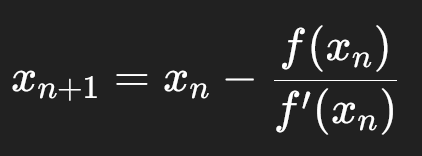Como referenciar este texto: ‘Método de Newton-Raphson: Um caminho gráfico até a solução’. Rodrigo Terra. Publicado em: 28/06/2025. Link da postagem: https://www.makerzine.com.br/dados/metodo-de-newton-raphson-um-caminho-grafico-ate-a-solucao/.
Conteúdos que você verá nesta postagem
Encontrar a raiz de uma função — ou seja, o valor de xxx que faz com que f(x)=0f(x) = 0f(x)=0 — é um dos problemas mais fundamentais e recorrentes da matemática. Ele está presente em diversas áreas do conhecimento: da física à economia, da engenharia à biologia. Resolver equações numericamente, quando não há solução exata ou quando ela é difícil de obter por métodos algébricos tradicionais, é uma habilidade essencial para quem trabalha com modelagem matemática.
Entre os diversos métodos numéricos disponíveis, o método de Newton-Raphson é um dos mais elegantes e eficientes. Baseado em aproximações sucessivas e no uso da derivada da função, ele parte de um chute inicial e, por meio de tangentes, caminha até uma raiz com rapidez impressionante — desde que certas condições sejam atendidas.
Apesar de ser amplamente ensinado em cursos de cálculo numérico, o método muitas vezes é apresentado de forma puramente algorítmica, com pouca ênfase em sua intuição geométrica. Mas é justamente essa dimensão visual que pode tornar o aprendizado mais claro, envolvente e memorável.
Foi pensando nisso que desenvolvi um projeto em Python que implementa o método de Newton-Raphson passo a passo e exibe graficamente cada uma de suas iterações. Em vez de apenas retornar a raiz final, o programa mostra como ela foi alcançada: os pontos de aproximação, as tangentes desenhadas a cada passo, o comportamento da função — tudo em um único gráfico. Essa visualização transforma o algoritmo em narrativa, revelando o caminho que o cálculo percorre até chegar à solução.
O Método Newton-Raphson
O método de Newton-Raphson é uma técnica numérica para encontrar raízes de funções reais com base em uma ideia simples, porém poderosa: usar a tangente de uma função como ponte até o zero do gráfico.
A lógica é a seguinte: dado um valor inicial x0, escolhemos um ponto na curva f(x) e traçamos a reta tangente naquele ponto. O ponto onde essa tangente intercepta o eixo x é a nossa próxima estimativa, x1. Repetimos esse processo — substituímos x0 por x1, traçamos a nova tangente e assim por diante — até que a aproximação tenda para uma raiz da função.
A fórmula usada em cada iteração é:
Esse cálculo depende de dois fatores principais:
O valor da função no ponto atual f(xn);
O valor da derivada nesse ponto f′(xn), que determina a inclinação da tangente.
Se a derivada for muito pequena (ou zero), o método pode falhar ou divergir. Mas quando bem aplicado, ele costuma convergir rapidamente — muitas vezes em poucas iterações — para a raiz mais próxima do chute inicial.
A beleza do Newton-Raphson está justamente em sua eficiência e na conexão entre análise numérica e geometria. Cada iteração é uma tangente, cada tangente é um passo em direção ao eixo x. E é essa trajetória, normalmente invisível nos cálculos, que o meu projeto se propõe a mostrar graficamente: uma sequência de pontos e retas que desenham o próprio raciocínio do método.
O Projeto em Python
Transformar o método de Newton-Raphson em código é um exercício direto, mas torná-lo visual e didático exige um pouco mais de cuidado — e foi exatamente essa a proposta deste projeto. O objetivo não era apenas encontrar a raiz de uma função, mas mostrar o caminho até ela, passo a passo, de forma interativa e compreensível.
O projeto foi implementado em Python com o apoio de três bibliotecas fundamentais:
sympypara interpretar a função simbólica fornecida pelo usuário e calcular automaticamente sua derivada;numpypara avaliação numérica dos pontos da função;matplotlibpara a criação dos gráficos, destacando os passos de aproximação, os pontos de interseção e as tangentes traçadas.
A implementação está organizada em duas funções principais:
newton_raphson_steps
Esta função recebe como entrada a expressão da função (em string), um valor inicial x0x_0x0, a tolerância desejada e o número máximo de iterações. Ela:
Converte a função em uma expressão simbólica;
Calcula sua derivada simbolicamente;
Avalia numericamente f(x) e f′(x) a cada iteração;
Aplica a fórmula de Newton-Raphson para gerar a próxima estimativa;
Armazena todos os passos da aproximação em uma lista.
O retorno inclui a raiz aproximada, a lista de todos os xnx_nxn calculados, e as funções numéricas que serão usadas para o gráfico.
plot_newton_raphson
Esta função é responsável pela parte visual. Ela:
Plota a curva da função original;
Destaca todos os pontos de aproximação (em vermelho);
Desenha retas tangentes que ilustram o raciocínio do método;
Marca o ponto final de convergência (em azul), mostrando a raiz encontrada.
O resultado é um gráfico que não apenas mostra onde está a raiz, mas também como o método chegou até ela — uma representação gráfica da sequência de ideias por trás do algoritmo.
Esse tipo de visualização transforma o Newton-Raphson em algo mais do que uma técnica numérica: ele se torna uma ferramenta narrativa, onde cada tangente conta um trecho da história até a solução.
Sobre o Código
O código que desenvolvi foi pensado para ser ao mesmo tempo funcional, didático e acessível. Ele está dividido em dois blocos principais, que se complementam: um responsável pelos cálculos e outro pela visualização gráfica. Essa separação permite compreensão modular do processo e facilita futuras adaptações.
Na função newton_raphson_steps, toda a lógica do método é organizada de forma transparente:
A função é recebida como uma string simbólica e convertida com
sympy, o que permite manipulação algébrica e diferenciação automática;A derivada é calculada simbolicamente e transformada em uma função numérica com
lambdify;A cada iteração, o novo valor de xxx é calculado e armazenado em uma lista — isso permite rastrear todo o caminho da convergência;
O processo é encerrado com base na tolerância (convergência) ou no número máximo de iterações, com mensagens claras para o usuário.
Já a função plot_newton_raphson cuida da visualização. Ela:
Plota o gráfico da função original em azul;
Destaca cada ponto de aproximação com marcadores vermelhos e linhas pontilhadas até o eixo;
Desenha tangentes verdes em cada passo, mostrando visualmente o cálculo da próxima estimativa;
Realça a última aproximação com um ponto azul, indicando a raiz final.
O gráfico é claro, limpo e expressivo. Com matplotlib, cada elemento visual foi cuidadosamente escolhido para não apenas ilustrar, mas ensinar: cada tangente conta uma parte da história da convergência, e cada ponto mostra onde o método apostou, acertou ou errou.
Além disso, o código está estruturado com parâmetros configuráveis (tolerância, número máximo de iterações, intervalo visual), comentários explicativos e exemplos prontos para teste. Tudo isso torna a ferramenta ideal tanto para uso individual quanto para aplicação em sala de aula, oficinas de programação matemática ou projetos de iniciação científica.
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
def newton_raphson_steps(expr_str, x0, tol=1e-6, max_iter=15):
x = sp.symbols('x')
f_expr = sp.sympify(expr_str)
df_expr = sp.diff(f_expr, x)
f = sp.lambdify(x, f_expr, 'numpy')
df = sp.lambdify(x, df_expr, 'numpy')
xn = x0
steps = [xn]
for n in range(max_iter):
fxn = f(xn)
dfxn = df(xn)
if abs(fxn) < tol:
print(f"Convergência atingida após {n} iterações.")
break
if dfxn == 0:
print("Derivada zero. Método falhou.")
break
xn = xn - fxn/dfxn
steps.append(xn)
else:
print("Máximo de iterações atingido. Método pode não ter convergido.")
return xn, steps, f, df
def plot_newton_raphson(expr_str, steps, f, df, padding=2.0):
raiz = steps[-1]
x_min = raiz - padding
x_max = raiz + padding
x_vals = np.linspace(x_min, x_max, 400)
y_vals = f(x_vals)
plt.figure(figsize=(10,6))
plt.plot(x_vals, y_vals, label='f(x)')
plt.axhline(0, color='black', linewidth=0.5)
for i in range(len(steps)-1):
xi = steps[i]
yi = f(xi)
plt.plot(xi, yi, 'ro')
plt.plot([xi, xi], [0, yi], 'r--', linewidth=0.8)
slope = df(xi)
tangent_x = np.linspace(xi-0.5, xi+0.5, 10)
tangent_y = yi + slope * (tangent_x - xi)
plt.plot(tangent_x, tangent_y, 'g--', linewidth=1)
plt.plot(steps[-1], f(steps[-1]), 'bo', label='Última aproximação')
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title(f"Newton-Raphson para {expr_str}\nRaiz aproximada: {raiz:.6f}")
plt.grid(True)
plt.show()
Casos de Uso e Interpretação Gráfica
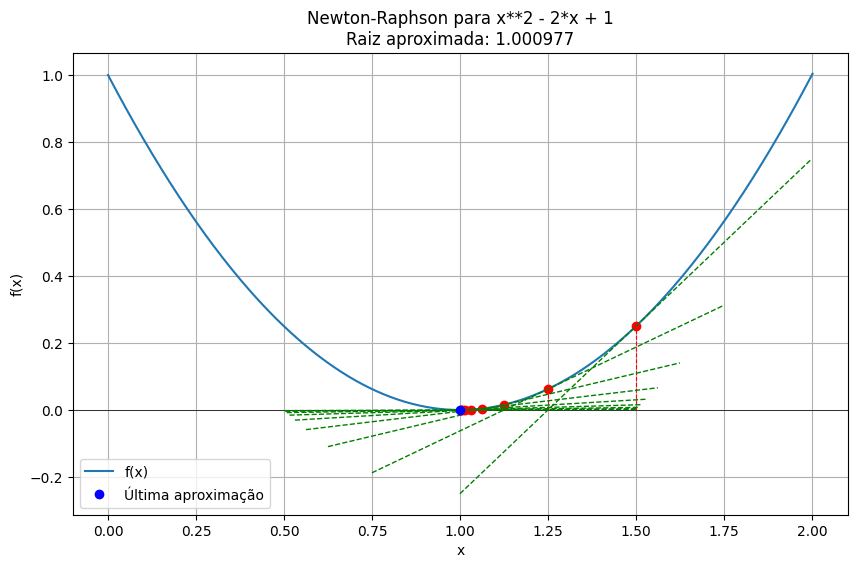
Essa função representa uma parábola com mínimo em x=1. A raiz exata da equação x2−2x+1=0 é justamente x=1, pois trata-se de um caso de raiz dupla (ou seja, o gráfico toca o eixo x, mas não o cruza).
No código, iniciei a aproximação com x0=1,5. O gráfico resultante mostra o ponto inicial em vermelho, seguido de retas tangentes verdes que conduzem suavemente até o vértice da parábola. Cada tangente representa uma tentativa de encontrar a raiz, e o ponto final azul destaca a última aproximação, já muito próxima da raiz exata.
Esse exemplo é ideal para visualizar o comportamento do método em funções suaves e bem comportadas. A convergência é rápida, e o gráfico reforça a intuição geométrica por trás do processo.
# Exemplo 1 de uso:
expr_str = "x**2 - 2*x + 1"
x0 = 1.5
raiz, passos, f, df = newton_raphson_steps(expr_str, x0)
plot_newton_raphson(expr_str, passos, f, df, padding=raiz)
print(f"Aproximação da raiz: {raiz}")
Convergência atingida após 9 iterações.
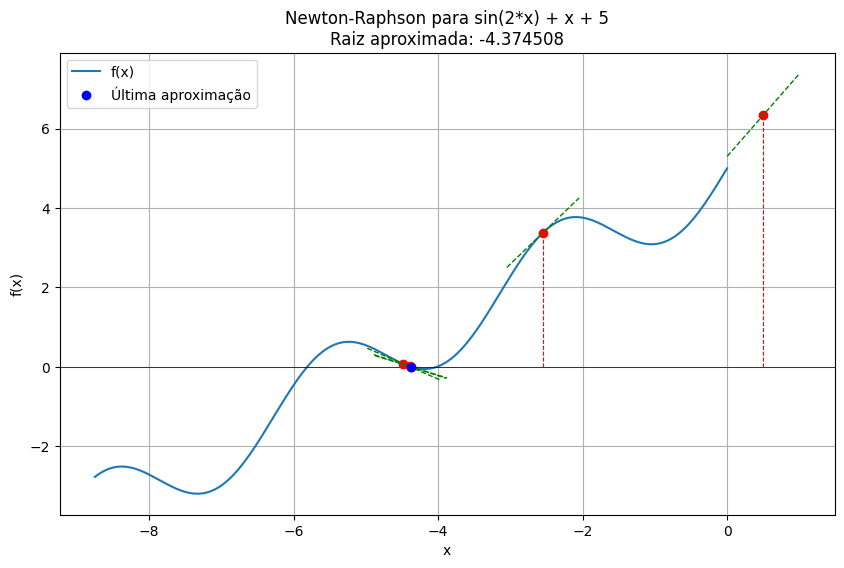
Neste caso, temos uma função mais complexa, com oscilação periódica (seno) e crescimento linear (termo x). A equação não possui raiz exata simples, o que torna o uso do método de Newton-Raphson ainda mais interessante.
Utilizei x0=0,5 como valor inicial. O gráfico mostra o comportamento ondulatório da função e como o método se adapta mesmo nesse cenário. As retas tangentes se ajustam às variações da curva, e a sequência de aproximações leva a um valor de raiz próximo de x=−4,37, com boa precisão.
Aqui, o gráfico também cumpre um papel pedagógico importante: mostra como o método pode lidar com funções não polinomiais, e como a escolha do valor inicial influencia o caminho (e o sucesso) da aproximação.
# Exemplo 2 de uso:
expr_str_2 = "sin(2*x) + x + 5"
x0 = 0.5
raiz, passos, f, df = newton_raphson_steps(expr_str_2, x0)
plot_newton_raphson(expr_str_2, passos, f, df, padding=raiz)
print(f"Aproximação da raiz: {raiz}")
Convergência atingida após 5 iterações.
Nos dois casos, a visualização gráfica ajuda a entender muito mais do que o resultado numérico. Ela revela o comportamento local da função, o papel da derivada, e os riscos de uma derivada nula ou mal condicionada. O que antes era uma sequência de números se transforma, com a ajuda do gráfico, em um raciocínio geométrico dinâmico.
Se você acha que este conteúdo pode ser útil para alguém, compartilhe!
Ao divulgar os textos do MakerZine, você contribui para que todo o material continue acessível e gratuito para todas as pessoas.