Como referenciar este texto: ‘Resolvendo um clássico com código: O problema das 8 rainhas’. Rodrigo Terra. Publicado em: 30/04/2025. Link da postagem: https://www.makerzine.com.br/dados/resolvendo-um-classico-com-codigo-o-problema-das-8-rainhas/.
Conteúdos que você verá nesta postagem
Imagine um tabuleiro de xadrez de 8×8 casas. Agora, tente colocar oito rainhas sobre ele de forma que nenhuma consiga atacar outra — nem na linha, nem na coluna, nem na diagonal. À primeira vista, pode parecer uma tarefa simples, mas logo se revela um desafio fascinante de lógica, paciência e estratégia.
Conhecido como o problema das 8 rainhas, esse clássico da matemática recreativa surgiu no século XIX e até hoje é estudado como uma introdução poderosa a conceitos de algoritmos e inteligência artificial. Mais do que apenas um enigma curioso, resolver o problema das 8 rainhas envolve explorar uma habilidade fundamental: a capacidade de voltar atrás, testar novas possibilidades e buscar caminhos alternativos — um processo conhecido como backtracking.
Neste artigo, vamos explorar como transformar esse desafio milenar em um projeto moderno de programação, visualizando cada tentativa e cada erro através de animações que mostram, passo a passo, o caminho até a solução.
Contexto Histórico
O desafio das 8 rainhas nasceu em 1848, proposto por Max Bezzel, um editor de xadrez alemão. Na época, o xadrez era mais do que um jogo: era uma metáfora para estratégia, lógica e a capacidade humana de pensar muitos passos à frente. Dentro desse espírito, Bezzel lançou o enigma: como posicionar oito rainhas em um tabuleiro padrão de xadrez de forma que nenhuma delas ameaçasse outra?
A princípio, o problema era tratado como uma curiosidade recreativa. No entanto, rapidamente chamou a atenção de matemáticos e entusiastas de lógica por sua profundidade inesperada. Entre os interessados, estava o renomado matemático Franz Nauck, que em 1850 não apenas encontrou soluções para o problema de 8 rainhas, mas também generalizou a questão para tabuleiros de qualquer tamanho — inaugurando o que hoje conhecemos como o problema das N rainhas.
O interesse pelo problema cresceu ao longo das décadas, impulsionado pela sua natureza desafiadora e pelo fato de que, apesar de simples de enunciar, sua resolução exige estratégias bastante sofisticadas. Ao longo do século XX, com o advento dos primeiros computadores, o problema das 8 rainhas se tornou um campo de testes natural para os novos conceitos de programação, algoritmos de busca e inteligência artificial.
Em 1950, Claude Shannon, considerado o pai da teoria da informação, citou problemas como o das 8 rainhas ao discutir estratégias de programação para jogos complexos. A partir da década de 1960, resolver problemas combinatórios como esse passou a ser uma área de estudo intensa em ciência da computação, especialmente no que se refere ao conceito de backtracking — a ideia de explorar uma possível solução, e se encontrar um obstáculo, “voltar atrás” para tentar outro caminho.
Hoje, o problema das 8 rainhas é muito mais do que um exercício de xadrez ou uma curiosidade matemática. Ele é um exemplo clássico de como a criatividade humana, aliada ao raciocínio estruturado, pode vencer desafios complexos. Além disso, serve como uma introdução prática a técnicas modernas que são fundamentais em áreas como algoritmos de busca, otimização, inteligência artificial e teoria da complexidade.
Ao explorarmos este problema, não estamos apenas resolvendo um enigma do século XIX: estamos, de certa forma, caminhando lado a lado com os grandes pensadores que ajudaram a construir as bases da programação e da computação moderna.
O Desafio: Regras e Objetivo
À primeira vista, o problema das 8 rainhas parece simples: basta posicionar oito peças em um tabuleiro de xadrez padrão (8 linhas por 8 colunas). No entanto, existe uma regra crucial que transforma o desafio em um verdadeiro exercício de lógica: nenhuma rainha pode atacar outra.
No xadrez, a rainha é a peça mais poderosa do jogo. Ela pode se mover qualquer número de casas:
Verticalmente (pela mesma coluna),
Horizontalmente (pela mesma linha),
Diagonalmente (em ambas as direções diagonais).
Portanto, para que duas rainhas coexistam pacificamente no tabuleiro, elas não podem compartilhar:
A mesma linha,
A mesma coluna,
Ou a mesma diagonal.
O objetivo é encontrar uma configuração de oito rainhas em que todas estejam protegidas — nenhuma ameaçando outra, nenhuma sendo ameaçada.
A complexidade surge justamente da interação entre essas restrições: posicionar uma rainha em um local estratégico pode abrir (ou fechar) possibilidades para todas as rainhas seguintes.
Visualizando o Problema:
Imagine que você acabou de posicionar a primeira rainha em uma casa qualquer. Instantaneamente, diversas casas são eliminadas como opções válidas: todas as casas da mesma linha, da mesma coluna e das duas diagonais que cruzam aquele ponto.
Agora, tente colocar a segunda rainha. O espaço seguro já é mais restrito. E cada nova rainha reduz ainda mais as opções disponíveis.
Assim, resolver o problema das 8 rainhas não é apenas sobre encontrar um espaço vazio — é sobre pensar estrategicamente, antecipar os impactos de cada movimento e, muitas vezes, reconhecer rapidamente quando é necessário recuar e tentar outra abordagem.
O que poderia ser resolvido de forma direta para dois ou três elementos, torna-se, com oito peças, um desafio onde a explosão de possibilidades exige método, paciência e inteligência.
Como Resolver? A Estratégia do Backtracking
Diante da explosão de possibilidades que o problema das 8 rainhas apresenta, a abordagem mais eficiente não é tentar prever todas as combinações possíveis — isso seria praticamente impossível até mesmo para os computadores mais rápidos. Em vez disso, usamos uma estratégia chamada backtracking: avançar com tentativas parciais e, sempre que encontramos um obstáculo, voltar atrás para corrigir o caminho.
O backtracking pode ser comparado a explorar um labirinto:
Em cada bifurcação, escolhemos um caminho e seguimos em frente.
Se chegarmos a um beco sem saída, voltamos até a última bifurcação e tentamos outra direção.
Repetimos esse processo até encontrar a saída — ou, no caso do nosso problema, até posicionar as oito rainhas com sucesso.
Aplicando essa lógica ao tabuleiro de xadrez:
Começamos posicionando uma rainha na primeira linha, escolhendo uma coluna que seja segura.
Em seguida, avançamos para a próxima linha e tentamos encontrar uma coluna livre, onde a nova rainha não esteja ameaçada pelas anteriores.
Se não for possível posicionar uma rainha em uma linha, sabemos que algo deu errado no caminho escolhido antes — então recuamos, retiramos a última rainha posicionada e tentamos outra opção.
Essa abordagem tem duas grandes vantagens:
Eficiência: Não precisamos verificar todas as 64⁸ combinações possíveis; exploramos apenas os caminhos viáveis.
Simplicidade: Apesar da complexidade aparente, o algoritmo de backtracking pode ser implementado de forma elegante e intuitiva, especialmente com o uso de recursão.
No fundo, o segredo para resolver o problema das 8 rainhas não está em prever todas as consequências antecipadamente, mas sim em adotar uma estratégia paciente e sistemática de tentativas, erros e correções. Cada volta atrás não é uma derrota, mas parte natural do processo que nos conduz à solução.
Mão na massa
Transformar a estratégia de backtracking em código foi o passo seguinte da jornada. Escolhi a linguagem Python, pela sua clareza e simplicidade para manipular estruturas como listas e recursão, e o ambiente Google Colab, que facilita experimentação rápida e visualização.
Estrutura do Algoritmo
O primeiro passo foi criar uma função que verifica se é seguro posicionar uma rainha em determinada posição. Para isso, o algoritmo precisa checar:
Se a coluna já está ocupada,
Se alguma das duas diagonais já tem uma rainha.
Se a posição for segura, posicionamos a rainha e seguimos para a linha seguinte. Caso não seja possível prosseguir, removemos a rainha anterior (backtracking) e tentamos a próxima opção disponível.
Todo o processo é conduzido de forma recursiva: cada linha tenta encontrar uma solução, e, ao encontrar um impasse, retorna para o passo anterior.
O Diferencial: Visualizar o Processo
Para tornar a resolução mais didática e visual, decidi criar animações que mostram cada passo do algoritmo:
Cada vez que uma rainha é colocada no tabuleiro, o movimento é desenhado.
Quando ocorre um backtrack, a remoção da rainha também é exibida.
Ao longo da execução, uma barra de progresso verde vai crescendo na parte inferior do tabuleiro, acompanhada de um contador percentual que mostra em que ponto da busca estamos.
Assim, em vez de simplesmente apresentar a solução final, podemos ver o algoritmo pensando, errando, corrigindo e, finalmente, triunfando — exatamente como acontece na lógica do backtracking.
Tecnologias Utilizadas
Matplotlib: Biblioteca gráfica usada para desenhar o tabuleiro, as rainhas e a barra de progresso.
Matplotlib Animation: Ferramenta para gerar a sequência animada dos movimentos e salvar como GIF.
ImageMagick: Utilizado no Google Colab para exportar o GIF final da animação.
Pequenos Aprimoramentos
Para deixar o projeto ainda mais completo, incluí:
Cores diferentes para representar rainhas iniciais, confirmações e backtracks,
Pausa de 2 segundos na solução final para melhor visualização,
Interpolação de frames entre movimentos para criar uma sensação de animação suave.
O resultado é uma representação viva do pensamento algorítmico: uma sequência de avanços e recuos orquestrados que, passo a passo, constrói a solução para o desafio das 8 rainhas.
Código
# Instalar imagemagick (uma vez no notebook)
!apt-get install imagemagick
# Importações
import matplotlib.pyplot as plt
from matplotlib import animation
from IPython.display import HTML, display
from google.colab import files
# Variáveis globais
states = []
actions = []
def save_state(board, action_type):
states.append([row.copy() for row in board])
actions.append(action_type)
def draw_board(state, action, ax, frame_idx, total_frames):
ax.clear()
# Desenhar o tabuleiro
for i in range(8):
for j in range(8):
color = 'white' if (i + j) % 2 == 0 else 'gray'
ax.add_patch(plt.Rectangle((j, 7-i), 1, 1, color=color))
# Desenhar rainhas
for i in range(8):
for j in range(8):
if state[i][j] == 1:
if action == "inicial" and states[0][i][j] == 1:
queen_color = 'blue'
elif action == "remover":
queen_color = 'gold'
else:
queen_color = 'red'
ax.text(j + 0.5, 7-i + 0.5, '♛', fontsize=24,
ha='center', va='center', color=queen_color)
# Barra de progresso SUAVE
progress = frame_idx / total_frames
ax.add_patch(plt.Rectangle((0, -0.5), 8 * progress, 0.3, color='green'))
# Texto do progresso
percent = int(progress * 100)
ax.text(4, -0.9, f"Progresso: {percent}%", fontsize=12,
ha='center', va='center', color='black')
ax.set_xlim(0, 8)
ax.set_ylim(-1.5, 8)
ax.axis('off')
def solve(board, row, colunas_ocupadas, diag1_ocupadas, diag2_ocupadas):
if row >= 8:
return True
if any(board[row]):
return solve(board, row + 1, colunas_ocupadas, diag1_ocupadas, diag2_ocupadas)
for col in range(8):
if not colunas_ocupadas[col] and not diag1_ocupadas[row + col] and not diag2_ocupadas[row - col + 7]:
board[row][col] = 1
colunas_ocupadas[col] = diag1_ocupadas[row + col] = diag2_ocupadas[row - col + 7] = True
save_state(board, "colocar")
if solve(board, row + 1, colunas_ocupadas, diag1_ocupadas, diag2_ocupadas):
return True
# backtrack
board[row][col] = 0
colunas_ocupadas[col] = diag1_ocupadas[row + col] = diag2_ocupadas[row - col + 7] = False
save_state(board, "remover")
return False
def main():
global states, actions
board = [[0 for _ in range(8)] for _ in range(8)]
print("Digite a posição inicial da primeira rainha:")
initial_row = int(input("Linha (1 a 8): "))-1
initial_col = int(input("Coluna (1 a 8): "))-1
if not (0 <= initial_row <= 7 and 0 <= initial_col <= 7):
print("Posição inválida!")
return
colunas_ocupadas = [False] * 8
diag1_ocupadas = [False] * 15
diag2_ocupadas = [False] * 15
board[initial_row][initial_col] = 1
colunas_ocupadas[initial_col] = True
diag1_ocupadas[initial_row + initial_col] = True
diag2_ocupadas[initial_row - initial_col + 7] = True
save_state(board, "inicial")
if solve(board, 0, colunas_ocupadas, diag1_ocupadas, diag2_ocupadas):
print("Solução encontrada!")
else:
print("Não foi possível encontrar uma solução a partir dessa posição.")
# DUPLICAR o último estado para "pausar" a solução final
num_copies = 6 # 4 cópias de 500ms = 2000ms
for _ in range(num_copies):
states.append(states[-1])
actions.append("final")
# INTERPOLAR frames para suavidade
frames_per_move = 5 # 5 frames suaves por ação
new_states = []
new_actions = []
for i in range(len(states) - 1):
for interp in range(frames_per_move):
new_states.append(states[i])
new_actions.append(actions[i])
# Adiciona o último frame
new_states.append(states[-1])
new_actions.append(actions[-1])
states[:] = new_states
actions[:] = new_actions
# Criar animação
fig, ax = plt.subplots()
def update(frame_idx):
draw_board(states[frame_idx], actions[frame_idx], ax, frame_idx, len(states)-1)
ani = animation.FuncAnimation(fig, update, frames=len(states), interval=100) # 100ms entre frames suaves
# Salvar como GIF
gif_path = "/content/solucao_8rainhas.gif"
ani.save(gif_path, writer='imagemagick', fps=10) # fps ajustado conforme suavidade
print(f"GIF salvo em: {gif_path}")
plt.close(fig)
# Mostrar o GIF
display(HTML(f'<img decoding="async" src="{gif_path}">'))
# Oferecer download
files.download(gif_path)
# Executar
animation_html = main()
Lógica utilizada:
Para resolver o problema das 8 rainhas, aplicamos uma estratégia conhecida como backtracking, que funciona como uma tentativa sistemática de construir uma solução válida, passo a passo, recuando sempre que encontramos um impasse.
O processo começa com a criação de um tabuleiro vazio 8×8, representado por uma matriz de zeros. O usuário é convidado a escolher a posição inicial da primeira rainha, que é fixada no tabuleiro. A partir daí, o algoritmo segue tentando posicionar uma nova rainha em cada linha subsequente. Para cada linha, ele percorre todas as colunas e verifica se a posição é segura — ou seja, se não existe nenhuma outra rainha já colocada na mesma coluna, na mesma diagonal principal ou na diagonal secundária. Essas verificações são feitas de maneira eficiente usando três listas auxiliares (colunas_ocupadas, diag1_ocupadas, diag2_ocupadas) que marcam rapidamente se uma coluna ou diagonal já está ameaçada.
Se encontrar uma posição segura, o algoritmo posiciona a rainha, registra o novo estado do tabuleiro, e avança para a próxima linha. Se não for possível colocar nenhuma rainha na linha atual, o algoritmo reconhece que chegou a um beco sem saída: ele então remove a última rainha colocada (fazendo o chamado backtrack), marca as colunas e diagonais como livres novamente, e tenta a próxima posição possível naquela linha anterior. Esse processo se repete recursivamente até que todas as oito rainhas sejam posicionadas corretamente ou até que todas as possibilidades sejam esgotadas.
Além de simplesmente encontrar a solução, o projeto registra todos os movimentos — tanto a colocação quanto a remoção de rainhas — para que possamos gerar uma animação mostrando o processo completo. Cada estado do tabuleiro é salvo logo após uma ação importante. No momento de desenhar, usamos o matplotlib para criar quadros visuais: desenhamos o tabuleiro, colocamos as rainhas nas suas posições respectivas, e adicionamos uma barra de progresso que cresce suavemente indicando o avanço da busca. Um contador de porcentagem também é exibido, ajudando a visualizar o quanto do processo já foi concluído.
Para tornar a animação mais agradável, interpolamos vários quadros entre cada movimento, criando a impressão de uma transição suave entre as ações. No final, o último estado (a solução completa) é mantido visível por alguns segundos extras, permitindo que o espectador aprecie a conquista antes que a animação recomece.
O resultado final é exportado como um arquivo GIF, pronto para ser visualizado ou compartilhado. Assim, transformamos a resolução de um clássico problema de xadrez não apenas em uma solução lógica elegante, mas também em uma jornada visual envolvente, onde cada tentativa, erro e correção se tornam parte da história que o algoritmo escreve até chegar à vitória.
Resultados
Ao executar o código acima e escolher a linha 3 e a coluna 3, vemos a saída:
Bem como o GIF é criado e baixado localmente:
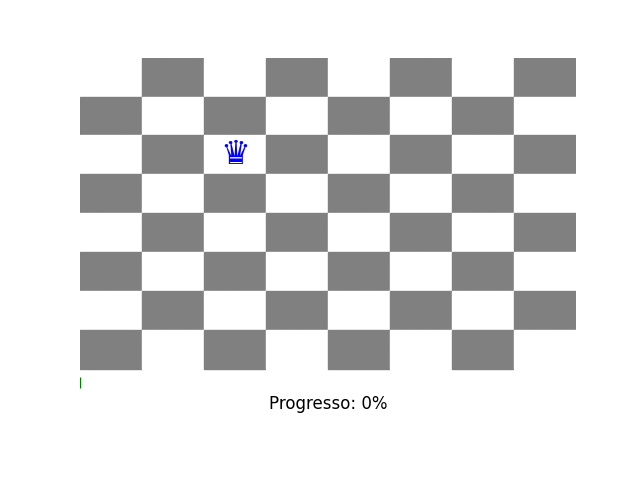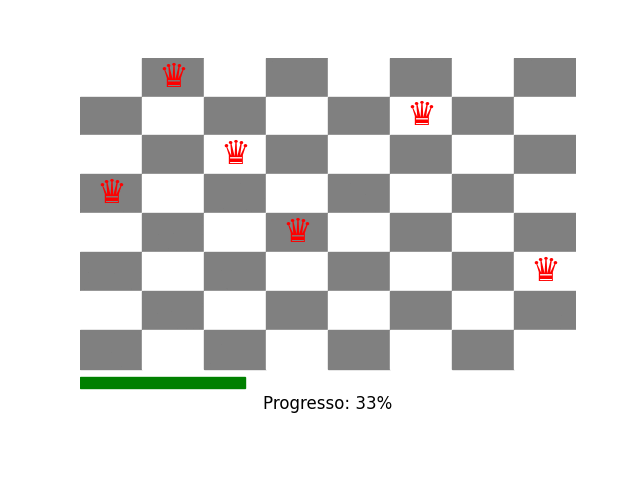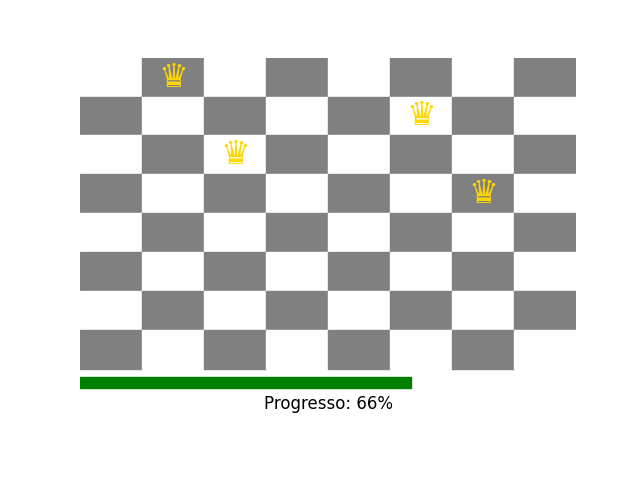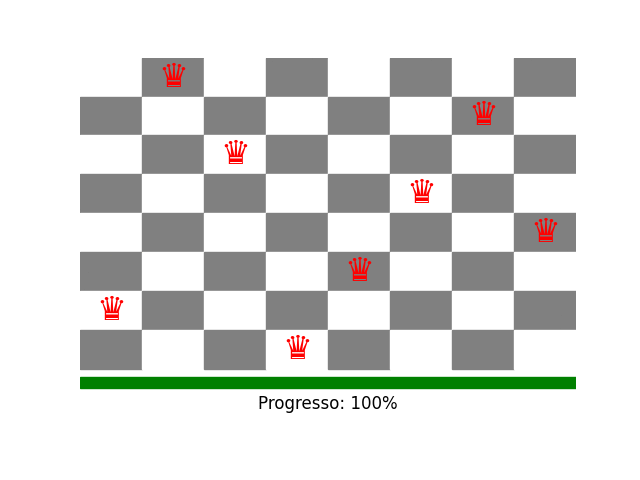
Se você acha que este conteúdo pode ser útil para alguém, compartilhe!
Ao divulgar os textos do MakerZine, você contribui para que todo o material continue acessível e gratuito para todas as pessoas.






