Física – Leis de Kirchhoff – 1ª Lei: Lei das Malhas (Plano de aula – Ensino médio)

Conceito e Lei das Malhas

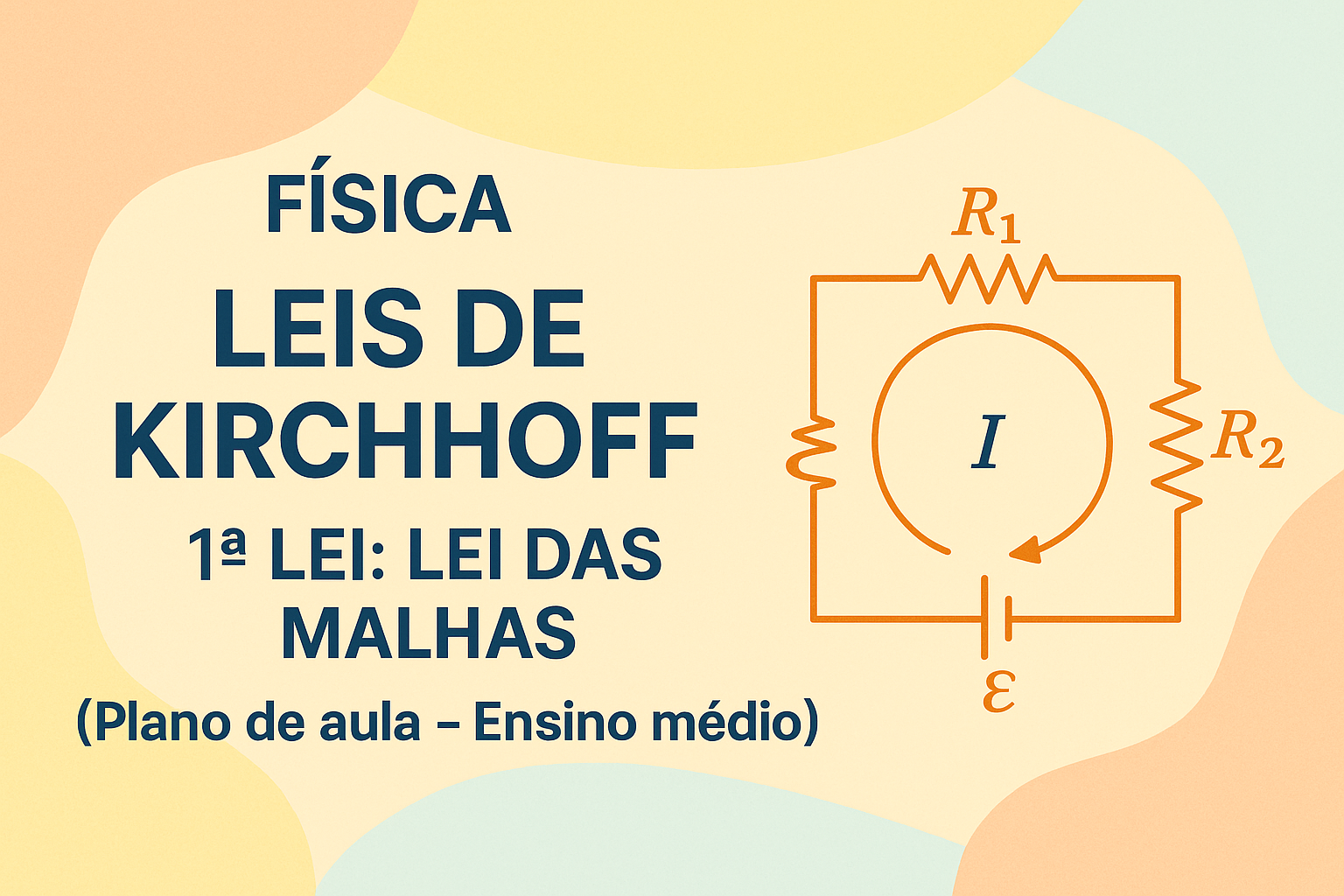
A Lei das Malhas afirma que a soma algébrica das tensões em uma malha fechada é igual a zero, o que decorre da conservação de energia em circuitos elétricos ideais. Ao escrever a expressão, consideramos o sentido de percurso e a convenção de sinais: se a malha é percorrida no sentido horário, as elevações de potencial são tratadas como positivas e as quedas como negativas.

\n\n

Essa lei se aplica independentemente do número de elementos na malha, desde que as fontes de energia estejam incluídas na soma. Em circuitos com várias tensões, a equação resultante descreve a soma de todas as contribuições de tensões e quedas de corrente ao longo do percurso escolhido.

\n\n

Para aplicar a Lei das Malhas, siga estes passos:

1. Defina o sentido de percurso da malha (geralmente no sentido horário).
2. Identifique cada componente e classifique como fonte de tensão (+) ou queda de tensão (-), escrevendo a expressão correspondente.
3. Some todas as tensões ao longo do percurso e iguale a zero, substituindo as quedas por termos como IR nos resistores.
4. Resolva a incógnita desejada e verifique se a soma é aproximadamente zero dentro de margens de erro.

\n\n

Em atividades de sala de aula, é comum verificar a Lei das Malhas com montagem simples: baterias, resistores e um multímetro para medir tensões. A prática reforça a concepção de conservação de energia, promove a integração entre Física, Matemática e Química e desenvolve habilidades de argumentação física e checagem de resultados.

Formulação matemática e notação

Matematicamente, para uma malha com n elementos, ΣV_i = 0 ao percorrer o ciclo fechado. Em cada elemento, V_i representa a variação de tensão ao longo daquele trecho: pode ser igual a I_j·R_j no caso de um resistor ou à variação de potencial de uma fonte.

A convenção de sinais é crucial; ao percorrer a malha no sentido horário, as quedas de tensão em elementos resistivos costumam ser registradas como V_i positivas, enquanto as elevações de potencial (quando o sentido de variação é contrário à direção de passagem) aparecem como negativas. Assim, a soma algébrica das tensões resulta em zero, refletindo o equilíbrio energético do ciclo.

Para montar uma equação de malha, rotule cada elemento com seu V_i, escreva a expressão correspondente (V_R = I·R para resistores, V_E para fontes com sinal adequado) e some ao redor da malha seguindo a direção escolhida. A incógnita típica é a(s) corrente(s) que percorre(m) a malha.

Em redes com várias malhas, o conjunto de equações de Kirchhoff é resolvido de forma simultânea. O método pode envolver substituição, eliminação ou álgebra linear (uso de matrizes). O objetivo é obter as correntes nos ramos e as tensões em cada elemento, mantendo a consistência com as leis da conservação.

Metodologia ativa para a aprendizagem

Metodologias ativas para a aprendizagem de física estimulam a participação dos estudantes, o raciocínio crítico e a colaboração entre pares. Em atividades de circuitos, a resolução de malhas em duplas com planejamento apoiado em planilhas de cálculo ajuda a tornar as soluções mais transparentes e justificadas.

Desenho de circuitos simples, simulação digital e validação prática permitem aos alunos experimentar a Lei das Malhas de forma contextualizada, verificando se a soma das tensões ao percorrer uma malha resulta em zero.

Essa abordagem favorece a construção de modelos mentais por meio de medições, comparação com valores teóricos e discussões para harmonizar diferentes caminhos de solução.

A integração entre Física, Matemática e Química com recursos abertos torna o conteúdo relevante para o cotidiano, conectando teoria, dados e situações reais.

A avaliação é formativa, baseada em rubricas de participação, resolução coletiva de problemas e explicação oral, com feedback que orienta o progresso dos estudantes.

Exemplos do cotidiano

Exemplos práticos: circuito de iluminação com três lâmpadas em uma malha única; variação de tensão com diferentes resistores e como a soma das quedas de tensão permanece constante. Nesses cenários, cada componente interrompe ou reduz o fluxo de energia, produzindo quedas proporcionais à resistência e à corrente.

\n\n

Ao observar situações reais, como o acendimento de várias lâmpadas em uma mesma fonte, o estudante visualiza a conservação de energia e a aplicação da Lei das Malhas. Ao percorrer a malha, a soma algébrica das tensões (quedas e geradas) se iguala à tensão da fonte, o que fica evidente mesmo com componentes diversos.

\n\n

Para consolidar o aprendizado, proponha resoluções de malhas em grupo, uso de planilhas simples para registrar as tensões em cada ponto da malha e validação experimental com multímetro. Discuta direções de referência, sinais de tensão positiva ou negativa e como a escolha da malha afeta a interpretação sem alterar o resultado físico.

\n\n

Essa abordagem não apenas fortalece a compreensão da Lei das Malhas, mas também conecta Física, Matemática e Química, mostrando que a ideia de balanço de energia aparece em circuitos do cotidiano, de fontes de iluminação a pequenos dispositivos eletrônicos, reforçando a relevância da teoria na prática.

Integração interdisciplinar

Integração com Matemática: uso de sistemas de equações lineares para resolver malhas complexas; com Química, conceitos de energia em sensores simples podem ser explorados em contextos laboratoriais; com História, a evolução da eletricidade e das leis de Kirchhoff pode enriquecer o quadro conceitual.

Essa interdisciplinaridade facilita a compreensão de modelos físicos como ferramentas matemáticas aplicadas à vida real.

Atividades práticas podem incluir a montagem de circuitos simples em protoboards ou simulações digitais, onde os alunos verificam que a soma das tensões ao longo de uma malha é igual a zero, mesmo com fontes de diferentes valores.

Para fortalecer o raciocínio físico, propõe-se abordagem de ensino ativo: resolução de malhas em grupo, registro de hipóteses, verificação experimental e discussão do significado das grandezas elétricas no dia a dia.

A integração entre Física, Matemática e Química é promovida por meio de planilhas de cálculo simples, recursos abertos e atividades contextualizadas, que aproximam o conteúdo da realidade cotidiana dos estudantes.

Materiais utilizados

Materiais básicos: pilhas/baterias, fios condutores, resistores de diferentes valores, interruptores, lâmpadas ou LEDs, multímetro, cartolinas para diagramas de malha e planilhas Google/Excel para cálculos.

Todos os itens são de fácil acesso e podem ser adquiridos ou reutilizados em diferentes salas de aula para reforçar a atividade prática.

Para organizar as atividades, proponha aos alunos montar circuitos simples com uma malha única e, em seguida, adicionar malhas adicionais para observar como as correntes e as tensões se distribuem. Use o multímetro para medir tensões em cada laço e comparar com os valores calculados.

Sugestões de registro: crie diagramas de malha em cartolina, transcreva os valores coletados em uma planilha, e utilize gráficos para representar a soma de tensões ao redor de cada malha. Enfatize a importância de fechar o circuito para a conservação da energia.

Questões de avaliação podem incluir a identificação de componentes com tolerância de resistência e a discussão de fontes de energia reais, como baterias, e como pequenas variações afetam a soma de tensões nas malhas.

Resumo para alunos

Esta seção apresenta a Lei das Malhas de Kirchhoff, com foco na primeira lei aplicada a circuitos elétricos. O objetivo é que o aluno compreenda por que, ao percorrer uma malha fechada, a soma das tensões é igual a zero, mesmo quando existem fontes de tensão de sinais diferentes ao longo do caminho.

Para iniciar a resolução, será adotada a convenção de sinais: correntes positivas em sentido definido, quedas de tensão positivas conforme a direção da travessia pela malha, e as tensões negativas quando o caminho encontra fontes opostas. Os alunos aprendem a construir malhas simples e a aplicar as equações resultantes para obter correntes e quedas de tensão.

Um componente essencial do plano é o uso de planilhas para calcular correntes e quedas de tensão em circuitos elementares. A atividade prática permite comparar resultados numéricos com medições conceituais, fortalecendo a validação experimental e o senso crítico físico.

Além disso, o plano promove integração entre Física, Matemática e Química, conectando conceitos a situações reais do cotidiano. Os alunos identificam erros comuns, discutem justificativas com base na conservação de energia e relatam as aprendizagens de forma contextualizada, reforçando a compreensão interdisciplinar.