Como referenciar este texto: ‘Regressão Linear do zero: Entendendo o passo a passo’. Rodrigo Terra. Publicado em: 23/04/2025. Link da postagem: https://www.makerzine.com.br/dados/regressao-linear-do-zero-entendendo-o-passo-a-passo/.
Conteúdos que você verá nesta postagem
A regressão linear é uma das ferramentas mais básicas (e poderosas!) da estatística e da ciência de dados. Neste texto, vamos construir uma regressão linear simples do zero, apenas com lógica matemática e programação, para entender como ela funciona por trás dos panos. Vamos usar o Python como aliado nesse processo.
O que é Regressão Linear?
A regressão linear é uma técnica que busca encontrar uma reta que melhor representa a relação entre duas variáveis. Por exemplo: será que existe uma relação entre o número de horas estudadas e a nota final de um estudante? A regressão linear tenta encontrar uma equação como:
y = a . x + b
Onde:
xé a variável independente (horas estudadas)yé a variável dependente (nota)aé o coeficiente angular (inclinação da reta)bé o intercepto (onde a reta cruza o eixo y)
Criando um exemplo simples
Vamos usar um pequeno conjunto de dados fictício:
# Dados simulados
x = [1, 2, 3, 4, 5]
y = [2, 4, 5, 4, 5]
Passo 1: Calculando os coeficientes da reta
Para encontrar os melhores valores de a e b, usamos as fórmulas:
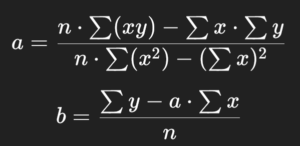
Vamos implementá-las:
n = len(x)
soma_x = sum(x)
soma_y = sum(y)
soma_xy = sum([x[i]*y[i] for i in range(n)])
soma_x2 = sum([xi**2 for xi in x])
a = (n * soma_xy - soma_x * soma_y) / (n * soma_x2 - soma_x**2)
b = (soma_y - a * soma_x) / n
Agora temos nossa reta!
Passo 2: Fazendo previsões
Vamos prever os valores de y com base na reta que encontramos:
y_pred = [a * xi + b for xi in x]
Passo 3: Calculando o erro (MSE)
Vamos medir o erro com o erro quadrático médio (MSE):
mse = sum([(y[i] - y_pred[i])**2 for i in range(n)]) / n
print(f"Erro quadrático médio: {mse:.2f}")
Usando nossos dados, o resultado apresentado foi:
Erro quadrático médio: 0.48
O Erro Quadrático Médio (MSE – Mean Squared Error) é uma métrica que indica o quão distantes, em média, as previsões do modelo estão dos valores reais.
Interpretação numérica
Esse valor significa que, em média, a diferença ao quadrado entre os valores previstos (
y_pred) e os reais (y) foi de 0.48.Como é uma média dos erros ao quadrado, valores mais altos indicam previsões mais imprecisas, e valores mais baixos indicam previsões mais próximas da realidade.
Como saber se 0.48 é bom ou ruim?
A interpretação depende da escala dos seus dados. Por exemplo:
Se seus valores de
yvariam entre 0 e 10, então um MSE de 0.48 é relativamente pequeno — mostra que o modelo está indo bem.Mas se seus valores de
yvariam entre 0 e 1, então 0.48 é grande, e indica que o modelo está com bastante erro.
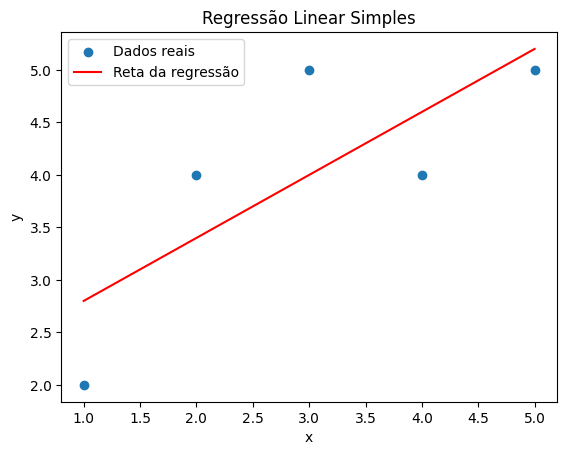
Passo 4: Visualizando o resultado
Por fim, vamos plotar os dados e a reta:
import matplotlib.pyplot as plt
plt.scatter(x, y, label="Dados")
plt.plot(x, y_pred, color='red', label="Reta da regressão")
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.title("Regressão Linear Simples")
plt.show()
Gráfico gerado:
Conclusão
Esse exercício mostra que é possível construir uma regressão linear com apenas lógica matemática e programação básica. Essa abordagem é ótima para ensinar os conceitos fundamentais por trás dos algoritmos que usamos em bibliotecas como scikit-learn ou statsmodels.
Se você acha que este conteúdo pode ser útil para alguém, compartilhe!
Ao divulgar os textos do MakerZine, você contribui para que todo o material continue acessível e gratuito para todas as pessoas.
