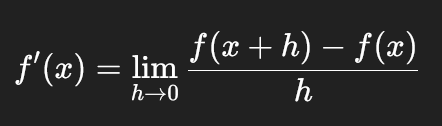Como referenciar este texto: ‘Derivando com Python: Encontrando a derivada pela definição’. Rodrigo Terra. Publicado em: 27/06/2025. Link da postagem: https://www.makerzine.com.br/dados/derivando-com-python-encontrando-a-derivada-pela-definicao/.
Conteúdos que você verá nesta postagem
Para muitos estudantes, o momento em que as derivadas aparecem nos livros de cálculo é marcado por dúvidas, ansiedade e uma avalanche de símbolos pouco familiares. Expressões como:
parecem mais enigmáticas do que esclarecedoras quando não há apoio visual ou prático. Compreender a derivada apenas como uma fórmula, sem ver seu efeito na forma da curva, pode transformar um conceito poderoso em uma barreira difícil de superar.
No entanto, a definição formal da derivada — baseada no limite do quociente incremental — é uma das ferramentas mais ricas para desenvolver o raciocínio matemático. Ela nos mostra, com precisão, como a variação instantânea de uma função pode ser obtida a partir de pequenos deslocamentos em torno de um ponto. É o ponto de partida para entender crescimento, mudança e comportamento local de uma função.
Foi justamente com esse olhar didático que nasceu este projeto: criar uma ponte entre a teoria e a prática por meio da programação. Desenvolvi um script em Python que calcula a derivada de qualquer função, não por meio de regras prontas, mas pela própria definição de limite. E mais: o código também gera gráficos da função original e da derivada, permitindo visualizar como cada curva se comporta e como estão relacionadas.
Esse recurso une três forças poderosas: a exatidão da matemática, a expressividade visual dos gráficos e a flexibilidade do código aberto. É uma forma de transformar um conteúdo abstrato em uma experiência concreta, explorável e compreensível.
Da Matemática Simbólica à Programação
A derivada, em seu conceito mais fundamental, expressa a taxa de variação de uma função em um determinado ponto. Embora nas aulas e nos livros ela costume ser ensinada por meio de regras diretas — derivada da potência, da soma, da exponencial, do seno, etc. — é a definição formal, baseada no limite, que revela com mais profundidade por que essas regras funcionam.
Mas nem sempre essa definição é fácil de acompanhar no papel. O raciocínio simbólico exige concentração, e o processo de substituir, manipular e simplificar expressões pode ser cansativo — ou até inacessível — para quem está aprendendo sozinho ou precisa de estímulos visuais. Foi aí que a programação entrou como uma aliada poderosa.
Com o auxílio da biblioteca SymPy, escrita em Python, é possível representar funções matemáticas de forma simbólica, assim como fazemos no papel. A diferença é que, ao programar, podemos pedir que o computador siga exatamente os passos da definição da derivada, sem atalhos. Ele substitui, calcula o quociente incremental, aplica o limite com h→0h \to 0 e simplifica a expressão — tudo isso em segundos, com precisão algébrica e transparência nos processos.
Essa ponte entre matemática simbólica e programação não apenas automatiza o cálculo, mas também explicita o raciocínio envolvido. A derivada deixa de ser uma resposta mágica no final de um cálculo e passa a ser o resultado natural de uma sequência de ideias — agora convertidas em lógica computacional.
A linguagem Python, por sua clareza e legibilidade, torna essa transição ainda mais fluida. Ela nos permite escrever o raciocínio quase como se estivéssemos conversando com o próprio conceito de derivada. E ao fazer isso, criamos um espaço de aprendizagem onde código e matemática se alimentam mutuamente.
O Projeto em Python
O coração do projeto é um script em Python capaz de receber qualquer função matemática como entrada, calcular sua derivada exatamente pela definição de limite e, em seguida, plotar os gráficos da função original e de sua derivada. É uma ferramenta que transforma uma fórmula abstrata em uma experiência visual e interativa.
A primeira etapa do código é interpretar a função digitada pelo usuário. Com a ajuda da biblioteca sympy, a expressão fornecida em forma de string (como "x**2 + 3*x + 2" ou "sin(x)") é transformada em uma entidade simbólica que pode ser manipulada como se estivéssemos fazendo álgebra no papel.
Em seguida, o script aplica a definição clássica da derivada:
Cada parte dessa expressão é calculada passo a passo. O código substitui xx por x+hx + h, monta o quociente incremental, e depois utiliza sympy.limit() para aplicar o limite quando hh tende a zero. O resultado é uma expressão simbólica da derivada, exata e pronta para uso — sem depender de regras prontas ou diferenciações automáticas.
Mas o projeto não para por aí. Após o cálculo simbólico, o script converte as expressões em funções numéricas com lambdify, e então usa a biblioteca matplotlib para gerar gráficos. O usuário pode ver, lado a lado, a curva da função original e a curva da derivada, sobre o mesmo eixo, com cores distintas e legenda clara. Essa visualização facilita enormemente a compreensão do que a derivada representa: a inclinação da tangente, a taxa de crescimento, as mudanças de concavidade.
Além disso, o código foi estruturado de forma modular, com funções bem definidas, comentários explicativos e parâmetros configuráveis. Isso permite que ele seja facilmente adaptado, reutilizado em outros projetos ou até transformado em um app visual com bibliotecas como Streamlit.
Esse projeto une precisão matemática, clareza computacional e poder visual — três elementos que, juntos, tornam o aprendizado mais acessível, mais intuitivo e muito mais envolvente.
Visualizando Conceitos com Código
Mais do que apenas calcular, este projeto tem como missão visualizar. A matemática, muitas vezes, é ensinada de forma abstrata, e isso pode dificultar a aprendizagem de conceitos fundamentais como o de derivada. Por outro lado, quando transformamos expressões simbólicas em curvas visíveis, compreensíveis e manipuláveis, abrimos novas portas para a intuição e a experimentação.
Ao exibir o gráfico de uma função e o da sua derivada no mesmo plano, o código convida o usuário a fazer perguntas como:
Onde a derivada é positiva ou negativa?
Em quais pontos a inclinação da curva é nula?
Como o comportamento da função (crescimento, decrescimento, concavidade) se relaciona com a forma da derivada?
Por exemplo, ao observar a parábola f(x)=x2f(x) = x^2, podemos ver graficamente que sua derivada f′(x)=2xf'(x) = 2x é uma reta que cruza a origem. A partir disso, fica fácil entender que a curva está decrescendo à esquerda do zero, crescendo à direita, e tem inclinação nula no vértice. Esses aspectos, que em sala de aula exigem muito esforço para serem explicados apenas com palavras e cálculos, se revelam com clareza em uma simples sobreposição de gráficos.
O uso de matplotlib para renderizar essas curvas torna o processo dinâmico e explorável. O usuário pode modificar a função, ajustar o intervalo de visualização e observar como a derivada se comporta. Cada mudança gera um novo par de gráficos — uma nova aula visual, construída em tempo real.
Essa abordagem também promove um aprendizado mais ativo. Em vez de decorar regras, o estudante experimenta, testa hipóteses, observa padrões e tira suas próprias conclusões. A derivada deixa de ser um conceito frio e passa a ser algo vivo, que responde a comandos e revela propriedades da função de forma concreta.
Sobre o Código
O código que desenvolvi é uma ferramenta educativa escrita em Python, pensada para mostrar, de forma clara e precisa, como funciona a definição de derivada no cálculo diferencial. O foco não está apenas no resultado final, mas no processo simbólico que leva até ele — exatamente como nos livros de matemática, mas com a velocidade e a transparência do código.
A estrutura do script é modular e objetiva. Ele começa solicitando do usuário uma função matemática em forma de string (por exemplo, "x**3 - x" ou "sin(x) + x**2"). Essa função é interpretada pela biblioteca sympy, que permite trabalhar com álgebra simbólica diretamente em Python — ou seja, em vez de números, manipulamos expressões exatas.
Esse processo é conduzido de forma simbólica e transparente: o código aplica substituições algébricas e calcula o limite de maneira explícita, como faríamos manualmente, mas com a eficiência e a precisão da automação. O resultado é a expressão da derivada simplificada, gerada passo a passo a partir da função original.
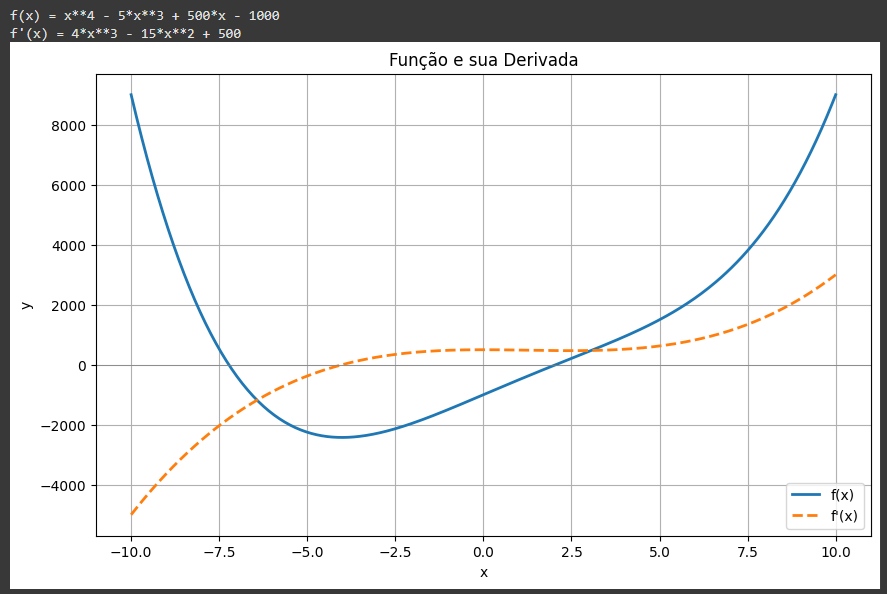
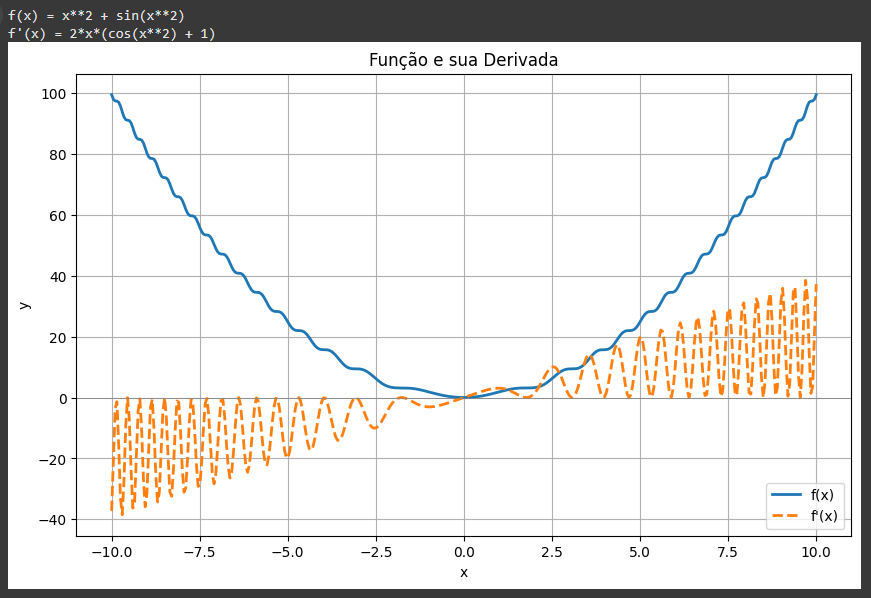
Com a derivada simbólica em mãos, o script avança para a visualização. Utilizando as bibliotecas numpy e matplotlib, ele transforma tanto a função quanto sua derivada em funções numéricas e plota ambas em um único gráfico. Cada curva é representada com cores e estilos diferentes, acompanhadas de rótulos, título e grade para facilitar a interpretação.
Esse recurso visual permite entender, de forma imediata, como a derivada se relaciona com o comportamento da função: onde cresce, onde decresce, onde a inclinação se anula. O código pode ser usado em sala de aula, como apoio ao ensino de cálculo, ou como ferramenta autônoma de estudo. Está bem estruturado, comentado e preparado para ser adaptado — seja para explorar novas funções, alterar intervalos ou incluir funcionalidades adicionais.
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
def derivada_pela_definicao(expr_str, variavel_str='x'):
x = sp.symbols(variavel_str)
h = sp.Symbol('h')
f = sp.sympify(expr_str)
# Derivada pela definição do limite
f_x_h = f.subs(x, x + h)
quociente = (f_x_h - f) / h
derivada = sp.limit(quociente, h, 0)
return f, derivada.simplify(), x
def plota_funcao_e_derivada(f_expr, derivada_expr, x_symbol, intervalo=(-10, 10), num_pontos=400):
# Converter expressões simbólicas em funções numéricas
f_lamb = sp.lambdify(x_symbol, f_expr, modules=['numpy'])
df_lamb = sp.lambdify(x_symbol, derivada_expr, modules=['numpy'])
# Criar os valores de x e calcular y para f(x) e f'(x)
x_vals = np.linspace(*intervalo, num=num_pontos)
y_vals = f_lamb(x_vals)
dy_vals = df_lamb(x_vals)
# Plotar os gráficos
plt.figure(figsize=(10, 6))
plt.plot(x_vals, y_vals, label='f(x)', linewidth=2)
plt.plot(x_vals, dy_vals, label="f'(x)", linestyle='--', linewidth=2)
plt.axhline(0, color='gray', linewidth=0.5)
plt.title('Função e sua Derivada')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()
# Exemplo 1 de uso
entrada = 'x**4 - 5*x**3 + 500*x -1000'
f_expr, derivada_expr, x = derivada_pela_definicao(entrada)
print(f"f(x) = {f_expr}")
print(f"f'(x) = {derivada_expr}")
plota_funcao_e_derivada(f_expr, derivada_expr, x)
# Exemplo 2 de uso
entrada = 'sin(x**2) + x**2'
f_expr, derivada_expr, x = derivada_pela_definicao(entrada)
print(f"f(x) = {f_expr}")
print(f"f'(x) = {derivada_expr}")
plota_funcao_e_derivada(f_expr, derivada_expr, x)
Se você acha que este conteúdo pode ser útil para alguém, compartilhe!
Ao divulgar os textos do MakerZine, você contribui para que todo o material continue acessível e gratuito para todas as pessoas.
