Como referenciar este texto: Análise Descritiva: Um guia inicial. Rodrigo Terra. Publicado em: 26/02/2024. Link da postagem: https://www.makerzine.com.br/python/analise-descritiva-descomplicada-conceitos-chave-e-aplicacoes.
Conteúdos dessa postagem
1. O que é Estatística?
A estatística é muito mais do que apenas números em tabelas ou gráficos, é uma poderosa ferramenta que nos permite navegar pelo vasto oceano de informações que nos cerca.
É a ciência por trás da coleta, análise, interpretação, apresentação e organização de dados, proporcionando-nos uma compreensão mais profunda do mundo ao nosso redor.
Mas por que precisamos tanto da estatística? Por que é essencial entender o que está por trás dos dados?
Essas são perguntas importantes que merecem ser exploradas. Ao compreender os princípios estatísticos, somos capacitados a tomar decisões informadas, identificar tendências, fazer previsões e tirar conclusões fundamentadas. Em um mundo inundado por informações, a estatística serve como bússola, guiando-nos na direção certa e ajudando-nos a discernir entre o significativo e o insignificante.
2. Medidas de tendência central
As medidas de tendência central indicam o valor central ou típico de um conjunto de dados. Elas são úteis para resumir e descrever a distribuição dos dados. As medidas de tendência central mais comuns incluem:
Média: Também conhecida como média aritmética, é calculada somando todos os valores dos dados e dividindo pela quantidade total de valores. É representada pelo símbolo “μ” (mi) para populações e “x̄” (x barra) para amostras.
Mediana: É o valor que divide o conjunto de dados em duas partes iguais, ou seja, 50% dos dados estão abaixo dela e 50% estão acima. É menos sensível a valores extremos do que a média e é geralmente preferida em distribuições assimétricas.
Moda: É o valor que ocorre com mais frequência em um conjunto de dados. Pode haver uma moda (unimodal), duas modas (bimodal) ou mais (multimodal), ou nenhuma moda se todos os valores forem diferentes.
2a. Média
A média, também conhecida como média aritmética, é uma das medidas de tendência central mais utilizadas para descrever um conjunto de dados. Ela é calculada somando todos os valores numéricos do conjunto de dados e dividindo essa soma pelo número total de valores. A média fornece um valor representativo que resume ou indica o “centro” do conjunto de dados. Aqui está como calcular a média, incluindo a equação:

Exemplo
Se você tem um conjunto de dados composto pelos valores 3,5,7,10,15, a média seria calculada da seguinte forma:
- Primeiro, some todos os valores: 3+5+7+10+15=40.
- Então, divida essa soma pelo número total de valores no conjunto, que é 5 neste caso: 40/5=8.
Portanto, a média desse conjunto de dados é 8.
A média é particularmente útil quando se deseja encontrar uma posição central que representa um conjunto de dados numéricos. No entanto, é importante notar que a média pode ser influenciada por valores extremamente altos ou baixos (valores discrepantes), o que pode torná-la menos representativa do conjunto de dados como um todo, especialmente quando a distribuição dos dados é muito assimétrica.
Exemplo em Python
Entrada
# Definindo o conjunto de dados
dados = [2, 4, 6, 8, 10]
# Calculando a média
media = sum(dados) / len(dados)
# Exibindo o resultado
print("O conjunto de dados é:", dados)
print("A média é:", media)
Saída
O conjunto de dados é: [2, 4, 6, 8, 10]
A média é: 6.0
2b. Mediana
A mediana é uma medida de tendência central que indica o valor central de um conjunto de dados quando esses dados são organizados em ordem crescente ou decrescente. Diferentemente da média, que soma todos os valores e divide pelo número total de observações, a mediana divide um conjunto de dados ordenados em duas partes iguais. Aqui estão os passos para calcular a mediana, incluindo fórmulas dependendo se o número de observações é ímpar ou par:
Se o número de observações for ímpar
- Organize os dados em ordem crescente ou decrescente.
- A mediana será o valor que está na posição central do conjunto de dados. A posição da mediana pode ser encontrada usando a fórmula: (n+1)/2, onde n é o número total de observações.

Exemplo para número ímpar de observações
Se você tem um conjunto de dados como 1,3,3,6,7,8,9, a mediana é 6, pois é o quarto número em um conjunto de sete números.
Se o número de observações for par
- Organize os dados em ordem crescente ou decrescente.
- A mediana será a média dos dois valores centrais. Para encontrar esses dois valores, use as posições n/2 e n/2+1, onde n é o número total de observações.
- Calcule a média desses dois valores centrais para obter a mediana.

Exemplo para número par de observações
Se você tem um conjunto de dados como 1,2,3,4,5,6,7,8, os dois valores centrais são 4 e 5. Portanto, a mediana é a média de 4 e 5, que é (4+5)/2=4,5.
Exemplo em Python
Entrada
# Exemplo em Python para calcular a mediana de um conjunto de dados
def calcular_mediana(dados):
# Ordena os dados
dados.sort()
# Calcula o número de observações
n = len(dados)
# Verifica se o número de observações é ímpar ou par
if n
# Para um número ímpar de observações, retorna o valor central
return dados[n // 2]
else:
# Para um número par de observações, retorna a média dos dois valores centrais
return (dados[n // 2 - 1] + dados[n // 2]) / 2
# Exemplo 1: Número ímpar de observações
dados_impar = [3, 1, 7, 9, 3, 6, 8]
mediana_impar = calcular_mediana(dados_impar)
# Exemplo 2: Número par de observações
dados_par = [1, 2, 3, 4, 5, 6, 7, 8]
mediana_par = calcular_mediana(dados_par)
mediana_impar, mediana_par
Saída
(6, 4.5)
2c. Moda
A moda é outra medida de tendência central, que identifica o(s) valor(es) mais frequente(s) em um conjunto de dados. Diferentemente da média e da mediana, a moda pode ser usada com dados numéricos, categóricos ou ordinais. Um conjunto de dados pode ter uma moda (unimodal), duas modas (bimodal), várias modas (multimodal) ou nenhuma moda, dependendo da frequência dos valores.
Não há uma “equação” específica para calcular a moda como há para a média ou a mediana, pois a moda é determinada pela frequência com que os valores ocorrem. No entanto, o processo para encontrar a moda em um conjunto de dados pode ser descrito da seguinte maneira:
- Liste todos os valores únicos no conjunto de dados.
- Conte quantas vezes cada valor ocorre para determinar a frequência de cada um.
- Identifique o valor com a maior frequência. Esse valor é a moda do conjunto de dados.
- Se dois ou mais valores compartilham a maior frequência, todos esses valores são considerados modas do conjunto.
Exemplos
- Conjunto de dados numérico: Para o conjunto [1,2,2,3,4], a moda é 2 porque o número 2 aparece com mais frequência do que os outros números.
- Conjunto de dados categórico: Para o conjunto [“vermelho”,”azul”,”azul”,”verde”], a moda é “azul” porque “azul” aparece mais frequentemente.
- Conjunto de dados bimodal: Para o conjunto [1,2,2,3,3,4], as modas são 2 e 3, pois ambos os números aparecem com a mesma frequência e mais frequentemente do que os outros números.
Exemplo em Python
Entrada
from collections import Counter
def calcular_moda(dados):
# Conta a frequência de cada valor no conjunto de dados
frequencias = Counter(dados)
# Encontra a máxima frequência
max_frequencia = max(frequencias.values())
# Encontra todos os valores que têm essa máxima frequência
modas = [valor for valor, freq in frequencias.items() if freq == max_frequencia]
# Retorna as modas
return modas
# Exemplo 1: Conjunto de dados numérico unimodal
dados_num_unimodal = [1, 2, 2, 3, 4]
moda_num_unimodal = calcular_moda(dados_num_unimodal)
# Exemplo 2: Conjunto de dados numérico bimodal
dados_num_bimodal = [1, 2, 2, 3, 3, 4]
moda_num_bimodal = calcular_moda(dados_num_bimodal)
# Exemplo 3: Conjunto de dados categórico
dados_cat = ["vermelho", "azul", "azul", "verde", "verde", "verde"]
moda_cat = calcular_moda(dados_cat)
moda_num_unimodal, moda_num_bimodal, moda_cat
Saída
([2], [2, 3], ['verde'])
3. Medidas de dispersão
As medidas de dispersão, também conhecidas como medidas de variabilidade, são estatísticas que descrevem quão espalhados estão os valores em um conjunto de dados. Elas fornecem uma noção da variabilidade dos dados em torno de uma medida de tendência central (como a média, mediana ou moda). As principais medidas de dispersão incluem o desvio padrão, a variância e a amplitude (ou intervalo). Cada uma dessas medidas oferece uma perspectiva diferente sobre a dispersão dos dados.
3a. Amplitude (Intervalo)
A amplitude, também conhecida como intervalo, é uma das medidas de dispersão mais simples para entender a variabilidade dentro de um conjunto de dados. Ela é calculada como a diferença entre o maior e o menor valor do conjunto. A amplitude oferece uma visão geral rápida da variação dos dados, mas como leva em consideração apenas os valores extremos, pode não representar adequadamente a variabilidade total do conjunto, especialmente em presença de valores discrepantes.
Cálculo da Amplitude
Para calcular a amplitude, você segue estes passos simples:
- Identifique o valor máximo (VmaxVmax) no conjunto de dados.
- Identifique o valor mínimo (VminVmin) no conjunto de dados.
- Subtraia o valor mínimo do valor máximo.

Cálculo da Amplitude
Considere o seguinte conjunto de dados, que representa, por exemplo, as temperaturas máximas diárias (em graus Celsius) em uma cidade durante uma semana: 25,28,31,29,32,30,27.
- O valor máximo (Vmax) é 32.
- O valor mínimo (Vmin) é 25.
- Calculando a amplitude: 32−25=7.
Portanto, a amplitude das temperaturas máximas durante essa semana é de 7 graus Celsius. Isso significa que a variação total nas temperaturas máximas durante a semana foi de 7 graus, do valor mais baixo ao mais alto.
Considerações
- Sensibilidade a Valores Discrepantes: A amplitude é muito sensível a valores discrepantes. Por exemplo, se em um dia houve uma temperatura anormalmente alta de 4040 graus devido a um evento atípico, a amplitude aumentaria significativamente, mesmo que o restante dos dados permanecesse consistente.
- Uso Limitado para Distribuições Largas: Para conjuntos de dados com distribuições largas ou com múltiplos picos, a amplitude pode não fornecer informações úteis sobre a dispersão geral dos dados, pois ignora a forma da distribuição.
Apesar dessas limitações, a amplitude é uma medida útil para uma avaliação rápida da variação em conjuntos de dados, especialmente quando combinada com outras medidas de dispersão, como o desvio padrão e o intervalo interquartil, para obter uma compreensão mais completa da variabilidade dos dados.
3b. Variância
A variância é uma medida de dispersão que indica quão espalhados estão os valores de um conjunto de dados em relação à sua média. Em outras palavras, ela mede o grau de variação dos dados, mostrando se os valores estão próximos uns dos outros (baixa variância) ou se estão mais espalhados (alta variância). A variância é um conceito fundamental em estatística e análise de dados, pois ajuda a entender a distribuição e a consistência dos dados.
Cálculo da Variância
A fórmula para calcular a variância (s²) depende de se você está lidando com uma amostra ou com uma população inteira.
Para uma população inteira, a variância (σ²) é calculada como:

Para uma amostra, a variância (s²) é calculada como:

A principal diferença entre as duas fórmulas é o denominador: n para população e n−1 para amostra, o último sendo um exemplo do uso da correção de Bessel, que corrige o viés na estimativa da variância da população a partir de uma amostra.
Exemplo
Suponha que temos um conjunto de dados representando as idades de um grupo de cinco amigos: 21,22,23,24,25.
Para calcular a variância dessas idades, primeiro encontramos a média:

Em seguida, usamos a fórmula da variância para uma amostra:

Portanto, a variância das idades neste exemplo é 2.52.5. Isso significa que, em média, as idades dos amigos variam 2.52.5 anos quadrados em relação à média de idade do grupo.
Considerações
- Unidade de Medida: Uma peculiaridade da variância é que ela é expressa no quadrado da unidade de medida dos dados (por exemplo, anos² para idades). Isso pode tornar a interpretação da variância menos intuitiva, razão pela qual o desvio padrão (a raiz quadrada da variância) é frequentemente usado para representar a dispersão dos dados em sua unidade original.
- Sensibilidade a Valores Discrepantes: Assim como outras medidas de dispersão, a variância é sensível a valores discrepantes, que podem inflar significativamente o valor da variância.
A variância é uma ferramenta essencial para a análise estatística, permitindo compreender como os dados se distribuem em torno da média e entre si.
3c. Desvio Padrão
O desvio padrão é uma medida de dispersão que indica o quanto os valores de um conjunto de dados variam ou se dispersam em relação à média (média aritmética). É uma das medidas mais importantes e amplamente utilizadas na estatística para quantificar a variabilidade ou volatilidade de um conjunto de dados. O desvio padrão ajuda a entender se os dados estão próximos uns dos outros (baixo desvio padrão) ou se estão mais espalhados (alto desvio padrão). Além disso, é útil para comparar a dispersão entre diferentes conjuntos de dados.
Cálculo do Desvio Padrão
A fórmula para calcular o desvio padrão varia ligeiramente dependendo de se está lidando com uma amostra ou com uma população inteira.
Para uma população inteira, o desvio padrão (σ) é calculado como a raiz quadrada da variância da população:

Para uma amostra, o desvio padrão da amostra (s) é calculado como a raiz quadrada da variância da amostra:

Exemplo
Vamos calcular o desvio padrão para o mesmo conjunto de dados do exemplo anterior, representando as idades de um grupo de cinco amigos: 21,22,23,24,25, onde a média é 23 e a variância da amostra (s²) é 2.5.
Para encontrar o desvio padrão da amostra (s), aplicamos a fórmula:
import math
# Variância da amostra do exemplo anterior
variancia_amostra = 2.5
# Cálculo do desvio padrão
desvio_padrao = math.sqrt(variancia_amostra)
desvio_padrao
E recebemos como saída:
1.5811388300841898
O desvio padrão das idades do grupo de amigos, com base na variância da amostra 2.5, é aproximadamente 1.58. Isso significa que, em média, as idades dos amigos variam 1.58 anos em relação à média de idade do grupo (23 anos).
Exemplo
- Interpretação: O desvio padrão é útil para entender a dispersão dos dados. Um desvio padrão baixo indica que os dados estão agrupados mais perto da média, enquanto um desvio padrão alto indica que os dados estão mais espalhados.
- Unidade de Medida: Ao contrário da variância, o desvio padrão é expresso na mesma unidade dos dados, facilitando sua interpretação. No exemplo acima, o desvio padrão é expresso em anos, assim como as idades originais.
- Uso: O desvio padrão é frequentemente usado em conjunto com a média para fornecer uma visão completa da distribuição dos dados. Por exemplo, em finanças, o desvio padrão dos retornos de um investimento é uma medida comum de risco.
O desvio padrão é uma ferramenta essencial para analisar a variabilidade dos dados, ajudando a tomar decisões informadas em diversos campos, como finanças, ciências, engenharia, e pesquisa social.
4. Percentil e Quartil
Percentis e quartis são medidas estatísticas que dividem um conjunto de dados ordenado em partes iguais, representando a posição relativa de um valor dentro desse conjunto. Eles são amplamente utilizados para avaliar a dispersão dos dados, entender a distribuição e identificar valores discrepantes.
4a. Percentil
Um percentil é uma medida que indica o valor abaixo do qual uma dada porcentagem dos dados no conjunto cai. Por exemplo, o 20º percentil é o valor abaixo do qual 20% dos dados podem ser encontrados. Isso significa que 80% dos dados estão acima desse valor. Os percentis são úteis para compreender a distribuição dos dados, além de serem frequentemente usados em testes padronizados e pesquisas de saúde para comparar pontuações individuais com uma população maior.
A fórmula para calcular a posição de um percentil específico PP em um conjunto de dados ordenado com n valores é:

Se a posição não for um número inteiro, interpola-se entre os valores para encontrar o percentil exato.
4b. Quartil
Os quartis são um caso específico de percentis que dividem os dados em quatro partes iguais. Existem três quartis principais:
- Primeiro Quartil (Q1 / 25º percentil): o valor abaixo do qual 25% dos dados caem. Ele divide o conjunto de dados no quartil inferior e os 75% restantes.
- Segundo Quartil (Q2 / 50º percentil ou Mediana): o valor que separa a metade inferior dos dados da metade superior. Ele é equivalente à mediana.
- Terceiro Quartil (Q3 / 75º percentil): o valor abaixo do qual 75% dos dados caem. Ele separa os 25% superiores dos dados do resto.
Para calcular os quartis, você organiza os dados em ordem crescente e aplica fórmulas específicas ou métodos de interpolação para encontrar os valores que dividem os dados nessas quartas partes iguais.
Exemplo
Considerando um conjunto de dados ordenado: 1,3,5,7,9.
- Q1 é o valor que divide os 25% inferiores dos dados. Neste caso, Q1 é 3.
- Q2 / Mediana é 5, pois divide o conjunto de dados ao meio.
- Q3 é 7, dividindo os 25% superiores dos dados.
Percentis e quartis são ferramentas essenciais para a análise exploratória de dados, fornecendo insights sobre a distribuição, identificando valores discrepantes e ajudando a entender melhor as características dos dados.
Exemplo em python
import matplotlib.pyplot as plt
import numpy as np
# Gerando um conjunto de dados aleatório
np.random.seed(0) # Para resultados reproduzíveis
dados = np.random.normal(loc=100, scale=20, size=200) # 200 pontos de dados com média 100 e desvio padrão 20
# Criando o gráfico boxplot
plt.figure(figsize=(10, 6))
plt.boxplot(dados, vert=True, patch_artist=True) # 'vert=True' para boxplot vertical; 'patch_artist=True' para preenchimento
plt.title('Boxplot de um Conjunto de Dados Aleatório')
plt.ylabel('Valores')
# Mostrando o gráfico
plt.grid(True)
plt.show()
e a saída, será:
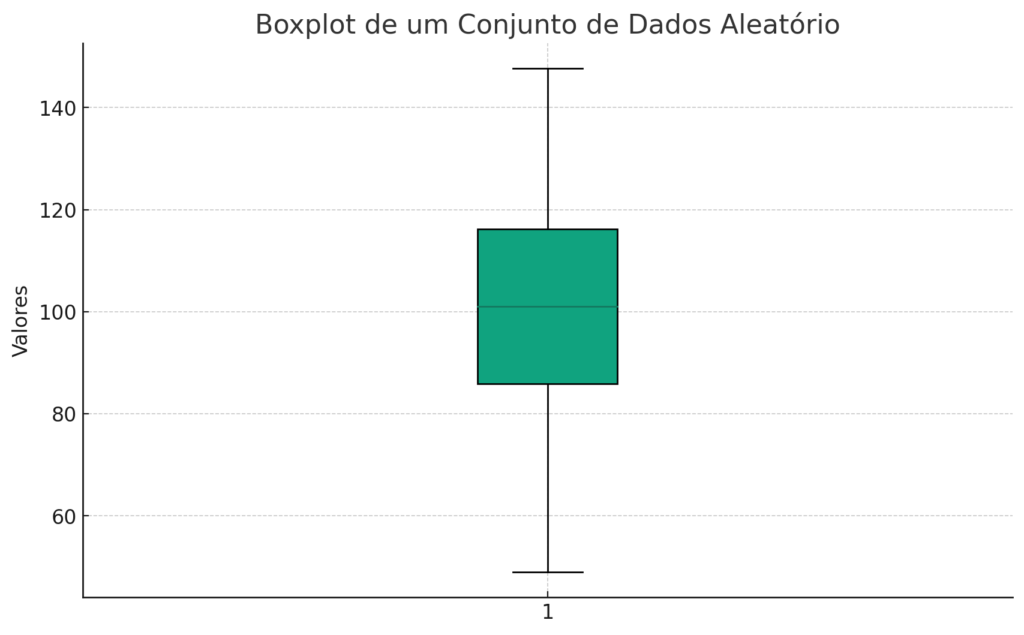
O gráfico boxplot acima ilustra a distribuição de um conjunto de dados aleatório com média 100100 e desvio padrão 2020, usando 200 pontos de dados. No boxplot, os quartis são representados da seguinte forma:
- A linha inferior da caixa indica o primeiro quartil (Q1), o valor abaixo do qual 25% dos dados caem.
- A linha no meio da caixa representa a mediana (Q2), dividindo o conjunto de dados ao meio. Esta é também a posição do segundo quartil.
- A linha superior da caixa indica o terceiro quartil (Q3), o valor abaixo do qual 75% dos dados caem.
As “antenas” ou “bigodes” que se estendem da caixa indicam a variabilidade fora dos quartis superiores e inferiores, enquanto os pontos fora dos bigodes podem ser considerados valores discrepantes.
Este gráfico é uma ferramenta poderosa para visualizar a dispersão dos dados, identificar valores discrepantes e entender a distribuição dos dados em termos de quartis.
4c. Intervalo interquartil
O Intervalo Interquartil (IIQ), também conhecido como amplitude interquartil, é uma medida de dispersão estatística que descreve a extensão da metade central de um conjunto de dados. Ele é calculado como a diferença entre o terceiro quartil (Q3) e o primeiro quartil (Q1), ou seja, mede a variação entre o 25º e o 75º percentil. O IIQ é uma ferramenta útil para avaliar a variabilidade dos dados, ignorando os 25% de dados mais baixos e os 25% de dados mais altos, o que o torna menos sensível a valores discrepantes do que outras medidas de dispersão, como a variância ou o desvio padrão.
Cálculo do Intervalo Interquartil
IIQ = Q3 – Q1
onde:- Q3 é o terceiro quartil, o valor abaixo do qual 75% dos dados caem,
- Q1 é o primeiro quartil, o valor abaixo do qual 25% dos dados caem.
Interpretação do Intervalo Interquartil
- Um IIQ pequeno indica que a metade central dos dados está agrupada mais de perto em torno da mediana, mostrando baixa variabilidade.
- Um IIQ grande indica que a metade central dos dados está mais espalhada, mostrando alta variabilidade.
Exemplo
Se temos um conjunto de dados: 1,2,3,4,5,6,7,8,9,
- O primeiro quartil (Q1) é 3, porque 25% dos dados são menores ou iguais a 3.
- O terceiro quartil (Q3) é 7, porque 75% dos dados são menores ou iguais a 7
Portanto, o IIQ seria 7−3=4. Isso significa que a metade central dos dados varia dentro de um intervalo de 4 unidades.
Uso do Intervalo Interquartil
- Identificar e avaliar a presença de valores discrepantes.
- Comparar a dispersão entre diferentes conjuntos de dados.
- Fornecer uma visão da variabilidade dos dados, complementando a mediana como medida de tendência central.
5. Z-Score
O Z-score, também conhecido como escore padrão, é uma medida estatística que descreve a posição de um valor individual em relação à média de um conjunto de dados, medido em termos de desvios padrão a partir dessa média. O Z-score é útil para determinar quão incomum ou comum é um valor dentro do conjunto de dados e para realizar comparações entre dados de diferentes grupos ou escalas.
5a. Cálculo do Z-Score
O Z-score de um valor é calculado usando a seguinte fórmula:

Interpretação do Z-score
- Z-score = 0: O valor X é igual à média do conjunto de dados.
- Z-score > 0: O valor X está acima da média do conjunto de dados.
- Z-score < 0: O valor X está abaixo da média do conjunto de dados.
- Quanto maior o valor absoluto do Z-score, mais distante o valor está da média, indicando que é menos comum.
Exemplo
Se um aluno obteve 85 pontos em um teste, onde a média da turma é 75 com um desvio padrão de 10, o Z-score do aluno pode ser calculado como:

Isso significa que a pontuação do aluno está 1 desvio padrão acima da média da turma.sso significa que a pontuação do aluno está 1 desvio padrão acima da média da turma.
5b. Uso do Z-score
O Z-score é amplamente utilizado em vários campos, incluindo:
- Estatística: Para identificar valores discrepantes.
- Finanças: Para avaliar o desempenho de um investimento em relação a um benchmark.
- Pesquisa: Para normalizar diferentes conjuntos de dados, permitindo comparações.
Um dos principais benefícios do Z-score é sua capacidade de permitir comparações entre dados de diferentes grupos, escalas ou distribuições, tornando-o uma ferramenta versátil e poderosa para análise estatística.
6. Assimetria
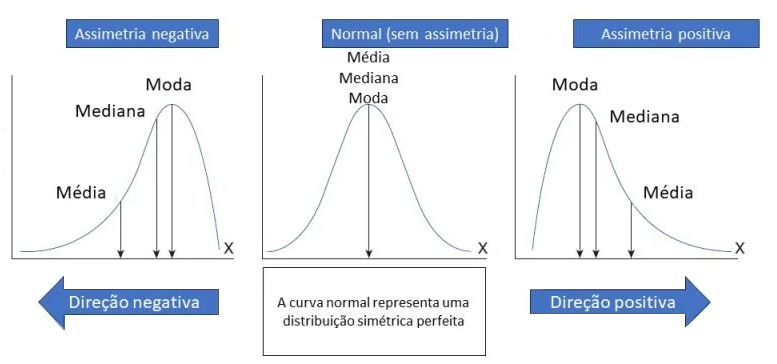
A assimetria, ou skewness, é uma medida estatística que descreve a extensão e a direção da distorção ou desvio da simetria em uma distribuição de frequência. Em uma distribuição perfeitamente simétrica, a média, mediana e moda dos dados coincidem e a curva da distribuição é igual em ambos os lados do ponto central. No entanto, na maioria das distribuições reais, essa simetria perfeita raramente ocorre, resultando em assimetria positiva ou negativa.
6a. Tipos de Assimetria
- Assimetria Positiva (Direita): Quando a cauda da direita da distribuição é mais longa ou estendida do que a da esquerda. Isso indica que há uma maior concentração de dados no lado inferior da distribuição. Neste caso, a média é tipicamente maior do que a mediana.
- Assimetria Negativa (Esquerda): Quando a cauda da esquerda da distribuição é mais longa ou estendida do que a da direita. Isso indica que há uma maior concentração de dados no lado superior da distribuição. Aqui, a média é tipicamente menor do que a mediana.
6b. Cálculo da Assimetria
A assimetria pode ser quantificada usando a seguinte fórmula:

O resultado desse cálculo indica a direção e a magnitude da assimetria. Um valor de assimetria de 0 indica uma distribuição perfeitamente simétrica. Valores positivos indicam assimetria à direita, enquanto valores negativos indicam assimetria à esquerda.
Interpretação da Assimetria
- Próximo de 0: A distribuição é aproximadamente simétrica.
- Positivo: Mais valores estão concentrados à esquerda do centro da distribuição, com a cauda se estendendo para a direita.
- Negativo: Mais valores estão concentrados à direita do centro da distribuição, com a cauda se estendendo para a esquerda.
6c. Importância da Assimetria na Análise de Dados
A assimetria é uma ferramenta importante na análise descritiva porque ajuda a entender a distribuição subjacente dos dados, o que é crucial para a seleção do método estatístico apropriado para análise. Por exemplo, muitos testes estatísticos assumem uma distribuição normal dos dados. Uma distribuição com assimetria significativa pode afetar a validade desses testes, levando a análises e conclusões incorretas. Além disso, entender a assimetria pode ajudar na tomada de decisões relacionadas ao tratamento de outliers e na aplicação de transformações para normalizar os dados.
7. Curtose
A curtose é uma medida estatística que descreve o grau de “pico” (ou apontamento) e “cauda” de uma distribuição de probabilidade em comparação com a distribuição normal (gaussiana). Ela fornece insights sobre a forma da distribuição dos dados, especialmente em termos de presença de outliers, pico da distribuição, e a propensão da distribuição a ter extremos. A curtose é uma característica importante da distribuição de um conjunto de dados porque influencia como os dados se espalham em torno da média.
7a. Tipos de Curtose
- Mesocúrtica: Uma distribuição mesocúrtica tem uma curtose similar à da distribuição normal, ou seja, tem um pico moderado e caudas de tamanho médio. A curtose de uma distribuição normal é definida como 0.
- Leptocúrtica: Uma distribuição leptocúrtica tem uma curtose maior do que a da distribuição normal. Isso significa que a distribuição tem um pico mais agudo e caudas mais pesadas. Distribuições leptocúrticas indicam uma maior probabilidade de outliers.
- Platicúrtica: Uma distribuição platicúrtica tem uma curtose menor do que a da distribuição normal, indicando um pico mais achatado e caudas mais curtas. Distribuições platicúrticas tendem a ter menos outliers do que a distribuição normal.

7b. Cálculo da Curtose
A curtose é calculada usando a seguinte fórmula:

O termo final é ajustado para que a curtose de uma distribuição normal seja zero. Assim, a curtose é frequentemente referida em relação à normalidade.
Interpretação da Curtose
- Curtose = 0: Indica uma curtose semelhante à da distribuição normal (mesocúrtica).
- Curtose > 0: Indica uma curtose maior que a normal, sugerindo um pico mais alto e caudas mais pesadas (leptocúrtica).
- Curtose < 0: Indica uma curtose menor que a normal, sugerindo um pico mais achatado e caudas mais curtas (platicúrtica).
7c. Importância da Curtose na Análise de Dados
A curtose é crucial para entender o comportamento dos dados, especialmente em relação à presença de outliers e ao risco associado a eventos extremos. Uma distribuição leptocúrtica, por exemplo, pode indicar um risco maior de outliers, o que é importante em campos como gestão de risco financeiro e controle de qualidade. Além disso, a compreensão da curtose pode ajudar na escolha de métodos estatísticos adequados para análise e na interpretação de resultados, especialmente em testes que assumem normalidade dos dados.
8. Correlação e Causalidade
Correlação e causalidade são dois conceitos fundamentais na estatística e pesquisa científica, frequentemente discutidos juntos para distinguir a natureza das relações entre variáveis. Embora ambos se refiram a conexões entre variáveis, eles têm significados e implicações muito diferentes.
8a. Correlação
A correlação refere-se a uma relação entre duas ou mais variáveis na qual elas se movem juntas de uma maneira previsível. Uma correlação pode ser positiva, negativa ou nula:
- Positiva: Quando uma variável aumenta, a outra também aumenta.
- Negativa: Quando uma variável aumenta, a outra diminui.
- Nula: Não há relação discernível na direção das variáveis.
Correlações são quantificadas através de coeficientes de correlação, como o coeficiente de correlação de Pearson, que varia de -1 a 1. Um valor de 1 indica uma correlação positiva perfeita, -1 indica uma correlação negativa perfeita, e 0 indica que não há correlação linear entre as variáveis.
Importante destacar que a correlação não implica causalidade. Ela simplesmente indica que há uma relação estatística entre as variáveis, mas não estabelece que uma variável causa a mudança na outra.

8b. Causalidade
Causalidade é a relação entre causa e efeito, onde uma variável (a causa) diretamente influencia outra variável (o efeito). Estabelecer causalidade implica que a mudança em uma variável é responsável pela mudança em outra. Diferente da correlação, que pode ser observada em dados correlacionados sem intervenção, a causalidade geralmente é determinada através de experimentação controlada ou análise longitudinal profunda, que pode controlar variáveis confundidoras.
8c. Distinção Importante
- Correlação é útil para identificar padrões e relações potenciais entre variáveis, o que pode ser um ponto de partida para investigações mais aprofundadas. No entanto, ela não pode, por si só, determinar se uma relação é de causa e efeito.
- Causalidade requer evidências mais fortes, geralmente obtidas por meio de experimentos controlados, onde o pesquisador manipula intencionalmente uma variável para observar o efeito em outra, enquanto controla outros fatores que podem afetar o resultado.
8d. Exemplo
Um exemplo clássico da distinção entre correlação e causalidade é a relação observada entre o consumo de sorvete e afogamentos. Os dados podem mostrar uma correlação positiva forte (i.e., ambos aumentam juntos durante os meses de verão), mas seria incorreto concluir que o consumo de sorvete causa afogamentos. Na realidade, uma variável confundidora (o clima quente) aumenta tanto o desejo de comer sorvete quanto a probabilidade de as pessoas nadarem, o que pode levar a mais afogamentos.
9. Análise de Outliers (Valores Discrepantes)
A análise de outliers (valores discrepantes) é uma parte crucial da análise de dados, envolvendo a identificação e o tratamento de observações que se desviam significativamente das outras observações em um conjunto de dados. Outliers podem influenciar significativamente os resultados de análises estatísticas e modelos preditivos, muitas vezes levando a conclusões enganosas. Por isso, é importante detectar e, se necessário, corrigir ou excluir outliers antes de proceder com análises mais detalhadas.

9a. Identificação de Outliers
Outliers podem ser identificados de várias maneiras, incluindo mas não limitado a:
- Desvio padrão: Uma observação pode ser considerada um outlier se estiver a mais de 2 ou 3 desvios padrão de distância da média.
- Intervalo interquartil (IQR): Observações que estão abaixo do primeiro quartil menos 1,5 vezes o IQR ou acima do terceiro quartil mais 1,5 vezes o IQR são frequentemente consideradas outliers.
- Gráficos Boxplot: Os boxplots visualizam a distribuição dos dados e destacam os outliers como pontos individuais fora dos “bigodes” do boxplot.
- Análise de resíduos em modelos de regressão: Resíduos que são significativamente maiores ou menores do que o esperado podem indicar a presença de outliers.
- Métodos baseados em distância ou densidade: Técnicas como DBSCAN (Density-Based Spatial Clustering of Applications with Noise) podem identificar outliers em conjuntos de dados multidimensionais.
9b. Impacto dos Outliers
O impacto dos outliers em uma análise pode variar:
- Estatísticas Descritivas: Podem distorcer médias, desvios padrão e outras medidas de tendência central e dispersão.
- Modelos Estatísticos: Podem afetar a precisão dos modelos de regressão, classificação e clustering, puxando a linha de regressão ou as fronteiras de decisão em direção a si mesmos.
- Inferência Estatística: Podem influenciar testes de hipóteses, levando a conclusões errôneas.
9c. Tratamento de Outliers
O tratamento adequado de outliers depende do contexto e dos objetivos da análise:
- Exclusão: Remover outliers pode ser justificável se houver certeza de que são devidos a erros de medição ou entrada de dados.
- Transformação: Aplicar transformações (logarítmica, raiz quadrada, etc.) pode reduzir o impacto de outliers sem removê-los.
- Imputação: Substituir outliers por valores medianos, médios, ou por meio de métodos de imputação mais sofisticados, pode ser adequado em alguns casos.
- Modelos Robustos: Utilizar modelos estatísticos ou algoritmos de machine learning que são menos sensíveis a outliers.
10. Gráficos e Visualizações
Gráficos e visualizações são ferramentas essenciais na análise de dados, permitindo aos analistas e ao público em geral entender complexidades e padrões nos dados de maneira intuitiva e direta. Eles transformam grandes conjuntos de dados e estatísticas numéricas em representações visuais que facilitam a identuição de tendências, outliers, e relações entre variáveis.
10a. Tipos de Gráficos e Visualizações
Existem diversos tipos de gráficos e visualizações, cada um adequado para diferentes tipos de dados e objetivos de análise:
Gráfico de Barras

Gráficos de barra são representações visuais de dados que utilizam barras retangulares para mostrar a relação entre diferentes categorias de dados. Cada barra representa uma categoria específica e sua altura ou comprimento é proporcional ao valor que está sendo representado. Geralmente, o eixo vertical (ou eixo y) representa a magnitude dos dados, enquanto o eixo horizontal (ou eixo x) mostra as categorias ou grupos aos quais os dados pertencem.
Os gráficos de barra são frequentemente utilizados para comparar quantidades entre diferentes categorias. Eles são particularmente eficazes para mostrar mudanças ao longo do tempo ou fazer comparações entre itens individuais. Esses gráficos são comumente encontrados em relatórios, apresentações e em diversos tipos de análises de dados, pois são fáceis de entender e interpretar.
Histogramas
Histogramas são uma representação visual de distribuição de dados que mostram a frequência com que certos valores ocorrem dentro de um conjunto de dados. Eles consistem em barras adjacentes, onde a área de cada barra é proporcional à frequência dos valores que ela representa.
Ao contrário dos gráficos de barra tradicionais, onde as categorias são distintas e independentes, os histogramas geralmente têm barras adjacentes, sem espaços entre elas, porque representam intervalos contínuos de valores. Eles são usados principalmente em estatísticas e análises de dados para visualizar a distribuição de uma variável numérica.
Os histogramas são úteis para entender a forma da distribuição dos dados, incluindo a presença de tendências centrais, dispersão, assimetria e outliers. Eles são comumente usados em áreas como ciência, engenharia, finanças, e muitas outras, para explorar e comunicar padrões nos dados.
Gráficos de Linhas

Gráficos de linhas são uma forma de representação visual de dados que utiliza linhas para mostrar a relação entre duas variáveis quantitativas, geralmente ao longo de um eixo temporal. Esses gráficos são úteis para destacar tendências e padrões ao longo do tempo ou em relação a alguma outra variável contínua.
Eles consistem em um sistema de coordenadas, onde os valores de uma variável são plotados ao longo de um eixo horizontal (geralmente o eixo x) e os valores correspondentes da outra variável são plotados ao longo do eixo vertical (geralmente o eixo y). Cada par de pontos de dados é então conectado por uma linha, mostrando a evolução ou relação entre os dados.
Os gráficos de linhas são comumente utilizados em várias áreas, como economia, ciências sociais, ciências naturais, engenharia, entre outras, para visualizar e analisar tendências ao longo do tempo, padrões sazonais, correlações entre variáveis, entre outros insights importantes. Eles são uma ferramenta valiosa para comunicação e análise de dados em muitos contextos.
Gráficos de Dispersão / Scatter Plots

Gráficos de dispersão são uma forma de visualização de dados que representa a relação entre duas variáveis quantitativas. Cada ponto no gráfico representa uma observação, com a posição do ponto determinada pelos valores das duas variáveis que estão sendo comparadas. Um eixo do gráfico representa uma variável, enquanto o outro eixo representa a outra variável.
Esses gráficos são particularmente úteis para identificar padrões ou relações entre duas variáveis, como correlações, tendências ou agrupamentos. Eles são frequentemente utilizados na análise exploratória de dados para detectar possíveis associações entre variáveis antes de realizar análises estatísticas mais detalhadas.
Além de revelar padrões ou tendências nos dados, os gráficos de dispersão também podem destacar pontos de dados incomuns ou outliers, que podem ser de interesse para investigação adicional.
Os gráficos de dispersão são comuns em áreas como ciências sociais, ciências naturais, economia, engenharia e muitas outras, onde a relação entre duas variáveis é de interesse para análise e interpretação.
Boxplot

Boxplots, também conhecidos como diagramas de caixa, são uma forma de visualização de dados que fornecem uma representação compacta da distribuição de uma variável numérica. Eles são compostos por cinco estatísticas resumidas: o mínimo, o primeiro quartil (Q1), a mediana (ou segundo quartil, Q2), o terceiro quartil (Q3) e o máximo.
A representação gráfica de um boxplot consiste em um retângulo (a “caixa”) que se estende do primeiro quartil ao terceiro quartil, com uma linha na mediana. As “linhas” que se estendem para fora da caixa (os “whiskers”) geralmente indicam o intervalo onde a maior parte dos dados se concentra, excluindo os valores extremos. Por vezes, os boxplots podem incluir também os outliers, representados por pontos ou asteriscos.
Boxplots são úteis para comparar a distribuição de uma variável entre diferentes grupos ou para visualizar a variabilidade dos dados em relação a uma medida central. Eles são frequentemente usados em estatísticas descritivas e análises exploratórias de dados, ajudando a identificar possíveis discrepâncias nos dados, assimetrias, e a presença de outliers.
Mapas de calor / Heatmaps

Úteis para visualizar a intensidade de fenômenos representados por cores, frequentemente usados em matrizes de correlação ou para representar dados em mapas geográficos.
Gráfico de Áreas

Mapas de calor (ou heatmaps) são uma forma de visualização de dados que representam a intensidade de uma variável em uma matriz bidimensional através de cores. Eles são frequentemente utilizados para visualizar a distribuição de valores em uma área geográfica ou em uma grade de células.
Na maioria dos casos, os mapas de calor atribuem uma cor a cada valor na matriz, com as cores variando de acordo com a intensidade ou magnitude da variável. Por exemplo, em um mapa de calor de temperatura, as cores mais quentes como vermelho ou amarelo podem representar temperaturas mais altas, enquanto as cores mais frias como azul ou verde podem representar temperaturas mais baixas.
Os mapas de calor são úteis para identificar padrões e tendências em conjuntos de dados grandes e complexos. Eles são amplamente utilizados em diversas áreas, incluindo análise de dados geoespaciais, visualização de padrões de tráfego em sites da internet, análise de padrões climáticos, análise de mercado, entre outras aplicações. Essa forma de visualização permite uma rápida identificação de áreas de alta ou baixa intensidade em uma grade de dados, facilitando a interpretação e a tomada de decisões com base nos dados apresentados.
Gráfico de Pizza / Pie Charts
Gráficos de pizza (ou gráficos de setores) são uma forma de visualização de dados que representam a distribuição proporcional de partes de um todo. Eles são chamados de “pizza” devido à sua semelhança com uma pizza dividida em fatias. Cada fatia do gráfico de pizza representa uma categoria de dados e o tamanho de cada fatia é proporcional à proporção dessa categoria em relação ao todo.
Os gráficos de pizza são mais eficazes quando há um número relativamente pequeno de categorias e quando essas categorias não possuem sobreposição significativa. Eles são úteis para destacar as partes que compõem um todo e para visualizar rapidamente as proporções relativas entre as diferentes categorias.
No entanto, é importante ter cautela ao usar gráficos de pizza, pois eles podem dificultar a comparação precisa entre as categorias e a leitura das proporções exatas, especialmente quando há muitas fatias ou quando as diferenças entre as proporções são sutis. Em algumas situações, gráficos de barras ou gráficos de linhas podem ser mais adequados para comunicar informações de forma mais clara e eficaz.
10b. Princípios de Boa Visualização
Para criar visualizações eficazes, é importante seguir alguns princípios:
- Clareza: O gráfico deve transmitir a informação de forma clara e direta, sem causar confusão.
- Simplicidade: Evitar elementos desnecessários que não acrescentam valor à interpretação dos dados.
- Precisão: As visualizações devem representar os dados de maneira precisa, sem induzir a interpretações erradas.
- Consistência: Usar estilos e cores de forma consistente para facilitar a compreensão.
- Contexto: Fornecer contexto adequado ao redor dos dados, incluindo títulos, legendas e notas explicativas quando necessário.
10c. Ferramentas de visualização
Existem várias ferramentas e bibliotecas disponíveis para a criação de gráficos e visualizações, tanto para usuários não técnicos quanto para desenvolvedores e analistas de dados, incluindo:
- Excel e Google Sheets: Ferramentas básicas com funcionalidades de gráficos para análises rápidas.
- Tableau e Power BI: Ferramentas de business intelligence que oferecem capacidades avançadas de visualização e interatividade.
- Python e R: Linguagens de programação com bibliotecas poderosas para visualização de dados, como Matplotlib, Seaborn, ggplot2, e Plotly.
11. Tabelas de Frequência
Tabelas de frequência são uma ferramenta fundamental na estatística descritiva, usadas para organizar e resumir dados. Elas mostram a distribuição de valores em um conjunto de dados, contabilizando quantas vezes cada valor ocorre (frequência). As tabelas de frequência facilitam a visualização de padrões, tendências e anomalias nos dados, tornando-se essenciais para a análise preliminar de dados em diversos campos, como sociologia, economia, psicologia, educação, e muitos outros.
11a. Tipos de Tabelas de Frequência
Existem dois tipos principais de tabelas de frequência:
- Tabelas de Frequência Absoluta: Mostram o número exato de vezes que cada valor ocorre no conjunto de dados.
- Tabelas de Frequência Relativa: Mostram a proporção ou percentagem que cada frequência representa no total de observações. Além disso, podem incluir frequências acumuladas, que somam as frequências de todas as classes até a classe atual, facilitando a compreensão da distribuição cumulativa dos dados.
11b. Como Construir uma Tabela de Frequência
Para construir uma tabela de frequência, siga estes passos:
- Coleta de Dados: Reúna e prepare os dados que serão analisados.
- Definição de Classes (para dados contínuos): Se os dados são contínuos, divida-os em intervalos ou classes. Para dados categóricos, cada categoria forma sua própria classe.
- Contagem de Frequências: Conte quantas vezes cada valor (ou intervalo de valores, para dados contínuos) ocorre no conjunto de dados.
- Cálculo de Frequências Relativas (Opcional): Converta as frequências absolutas em relativas, dividindo cada frequência pelo total de observações.
- Adição de Frequências Acumuladas (Opcional): Calcule as frequências acumuladas somando as frequências de todas as classes anteriores até a classe atual.
11c. Exemplo
Imagine um conjunto de dados contendo as notas de uma prova variando de 0 a 10 de 30 alunos. Uma tabela de frequência pode ser usada para sumarizar quantos alunos obtiveram cada nota, assim como a proporção de alunos que obtiveram notas até determinado ponto.
11d. Vantagens das Tabelas de Frequência
- Simplificação dos Dados: Tabelas de frequência resumem grandes volumes de dados de forma que padrões e tendências se tornem mais aparentes.
- Facilitação da Análise: Ajudam na identificação rápida de distribuições, modas e possíveis outliers.
- Base para Outras Análises: São fundamentais para a construção de gráficos, como histogramas e boxplots, e para cálculos estatísticos mais complexos.
12. Testes de Normalidade
Testes de normalidade são procedimentos estatísticos usados para determinar se um conjunto de dados segue uma distribuição normal (distribuição gaussiana). Esses testes são fundamentais em estatísticas, pois muitos métodos estatísticos, como os testes t e ANOVA, assumem que os dados seguem uma distribuição normal. Portanto, verificar essa suposição é um passo crucial antes de aplicar esses métodos.
12a. Por Que a Normalidade É Importante?
A distribuição normal é uma das distribuições mais comuns em estatísticas devido ao Teorema Central do Limite, que afirma que, sob certas condições, a média de uma amostra de observações independentes tende a seguir uma distribuição normal, independentemente da distribuição da população original. Isso torna a análise mais simples e os resultados mais confiáveis, desde que os dados sigam essa distribuição.
12b. Testes Comuns de Normalidade
Existem vários testes para verificar a normalidade de um conjunto de dados, incluindo:
- Teste de Shapiro-Wilk: Um dos testes mais poderosos para amostras pequenas a moderadas. Calcula um valor W que testa se uma amostra vem de uma população normalmente distribuída.
- Teste de Kolmogorov-Smirnov (K-S): Compara a distribuição cumulativa dos dados com a distribuição cumulativa esperada de uma distribuição normal. Pode ser usado para comparar duas amostras.
- Teste de Anderson-Darling: Similar ao teste K-S, mas dá mais peso às caudas da distribuição dos dados, sendo mais sensível a desvios nessas áreas.
- Teste de D’Agostino-Pearson: Baseia-se no cálculo do excesso de curtose e da assimetria dos dados para avaliar a normalidade.
Interpretando os Resultados
Os testes de normalidade geralmente fornecem um valor-p, que é usado para decidir se a hipótese nula (de que os dados seguem uma distribuição normal) pode ser rejeitada. Um valor-p baixo (tipicamente menor que 0,05) indica que os dados não seguem uma distribuição normal, sugerindo que métodos alternativos devem ser considerados.
12c. Limitações
- Sensibilidade com Grandes Amostras: Testes de normalidade podem se tornar muito sensíveis com grandes amostras, detectando pequenos desvios da normalidade que podem não ser relevantes na prática.
- Incapacidade de Detectar Todas as Formas de Não Normalidade: Alguns testes podem não detectar certos tipos de desvios da normalidade, especialmente em distribuições com formas peculiares.
12d. Alternativas
Quando os dados não são normalmente distribuídos, os pesquisadores podem recorrer a métodos não paramétricos, que não fazem suposições específicas sobre a forma da distribuição dos dados, ou podem aplicar transformações aos dados (como logarítmica ou de raiz quadrada) para tentar normalizar a distribuição.
13. Exploração Multivariada
A exploração multivariada de dados refere-se à análise estatística que envolve múltiplas variáveis ao mesmo tempo. Essa abordagem é crucial para entender as relações complexas entre diferentes variáveis em um conjunto de dados. Ao contrário da análise univariada, que examina cada variável isoladamente, ou da análise bivariada, que explora a relação entre duas variáveis, a exploração multivariada busca padrões e conexões entre três ou mais variáveis simultaneamente. Essa análise pode revelar insights que não seriam visíveis ao examinar as variáveis separadamente.
13a. Técnicas de Exploração Multivariada
Várias técnicas estatísticas são utilizadas para a exploração multivariada, cada uma adequada para diferentes tipos de dados e objetivos de análise:
- Análise de Componentes Principais (PCA): Reduz a dimensionalidade dos dados ao transformar variáveis correlacionadas em um número menor de variáveis não correlacionadas chamadas componentes principais. Isso ajuda a identificar as direções de maior variação nos dados.
- Análise de Agrupamento (Cluster Analysis): Agrupa os dados em clusters com base em suas semelhanças. Técnicas comuns incluem K-means, agrupamento hierárquico e DBSCAN. É útil para identificar padrões naturais ou segmentos nos dados.
- Análise de Fatores: Semelhante à PCA, busca identificar as variáveis latentes não observadas (fatores) que explicam padrões de correlação entre variáveis observadas. É frequentemente usada em psicometria e ciências sociais.
- Análise Discriminante: Utilizada para determinar quais variáveis discriminam entre duas ou mais classes naturais nos dados. É especialmente útil para classificação e previsão.
- Análise de Correspondência: Uma técnica usada para explorar as relações entre duas ou mais variáveis categóricas, representando graficamente suas interdependências.
- Regressão Múltipla: Avalia a relação entre uma variável dependente e várias variáveis independentes. Ajuda a entender como o valor da variável dependente muda quando qualquer uma das variáveis independentes é variada.
13b. Importância da Exploração Multivariada
- Descoberta de Padrões Complexos: Pode revelar interações entre variáveis que não são aparentes em análises menos complexas.
- Redução de Dimensionalidade: Ajuda a simplificar os dados ao identificar as principais variáveis que explicam a maior parte da variação nos dados, facilitando a visualização e análise subsequentes.
- Melhoria da Precisão Analítica: Ao considerar múltiplas variáveis simultaneamente, a análise multivariada pode melhorar a precisão de modelos preditivos e de classificação.
- Tomada de Decisão Informada: Fornece uma base sólida para tomar decisões informadas em campos como marketing, finanças, saúde e pesquisa social.
13c. Desafios
- Complexidade Computacional: A análise multivariada pode ser computacionalmente intensiva, especialmente com grandes conjuntos de dados.
- Interpretação dos Resultados: Os resultados de técnicas multivariadas podem ser difíceis de interpretar, exigindo um conhecimento sólido de estatísticas e da área de aplicação.
- Qualidade dos Dados: A precisão das análises multivariadas depende da qualidade dos dados de entrada, incluindo a necessidade de tratamento de dados ausentes e outliers.